Comprendre les Propriétés des Droites Parallèles et Perpendiculaires
Théorie
Droites Parallèles
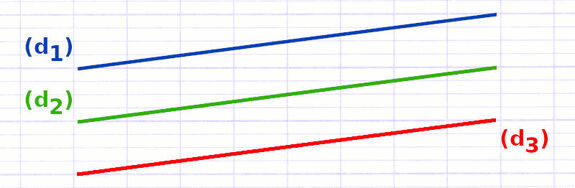
Propriété : Si 2 droites sont parallèles, alors une 3ème droite parallèle à l’une est également parallèle à l’autre.
Cette propriété s’applique lorsqu’une droite (d2) est parallèle à 2 autres droites (d1) et (d3).
Les droites (d1) et (d2) sont parallèles. La droite (d2) est également parallèle à la droite (d3). La droite (d3) est donc parallèle à la droite (d1).
Droites Parallèles et Perpendiculaires
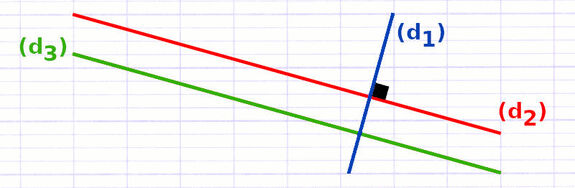
Propriété : Si 2 droites sont parallèles, alors une 3ème droite perpendiculaire à l’une est perpendiculaire à l’autre.
Cette propriété s’applique lorsqu’une droite (d1) est parallèle à une droite (d2) et perpendiculaire à une droite (d3).
Les droites (d1) et (d2) sont parallèles. La droite (d3) est perpendiculaire à la droite (d1). La droite (d3) est également perpendiculaire à la droite (d2).
Droites Perpendiculaires
Propriété : Si 2 droites sont perpendiculaires à une même droite, alors ces 2 droites sont parallèles.
Cette propriété s’applique lorsqu’une droite (d3) est perpendiculaire à 2 autres droites (d1) et (d2).
Les droites (d1) et (d2) sont perpendiculaires à la droite (d3). Ces 2 droites sont donc parallèles.
Exercice
Question 1
Sachant que (d2) est parallèle à (d3) et que (d2) est perpendiculaire à (d1), quelle est la particularité des droites (d3) et (d1) ?
Question 2
Si deux droites sont perpendiculaires à une même droite, alors ces deux droites sont ___.
Question 3
Sachant que (d1) est parallèle à (d2) et que (d3) est parallèle à (d1), quelle est la particularité des droites (d3) et (d2) ?