Comprendre et Utiliser un Ratio
Théorie
Un ratio indique le rapport entre deux grandeurs (ou plus). En mathématiques, une grandeur désigne tout ce qui peut se mesurer ou se calculer (une quantité, une longueur, un prix...).
Ratio 2 : 1
Le ratio 2 : 1 indique que le rapport entre deux grandeurs est de 2 pour 1. Dans un sac, des boules bleues et jaunes sont dans un ratio 2 : 1 s’il y a deux boules bleues pour une boule jaune. Le ratio 2 : 1 indique donc qu’il y a deux fois plus de boules bleues (grandeur 1) que de boules jaunes (grandeur 2).
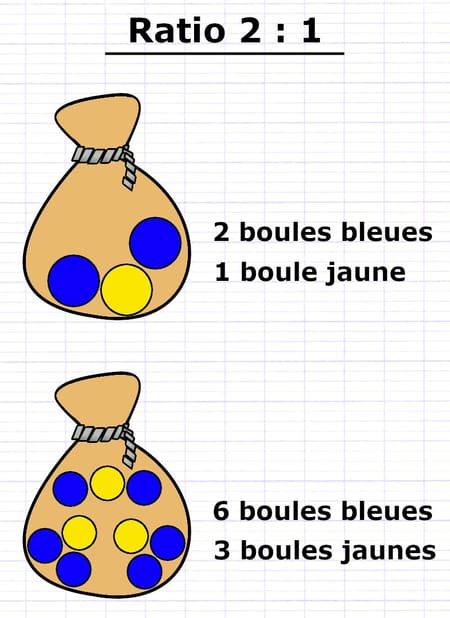
Les boules bleues et jaunes sont dans un ratio 2 : 1 dans chaque sac.
La proportion de chaque grandeur dans un ratio 2 : 1 peut s’écrire à l’aide d’une fraction :
- Le numérateur est l’un des nombres du ratio : 2 (grandeur 1) ou 1 (grandeur 2).
- Le dénominateur est la somme des nombres du ratio : 3 (2 + 1).
Si les boules bleues et jaunes sont dans un ratio 2 : 1, alors :
- 2/3 des boules sont bleues.
- 1/3 des boules sont jaunes.
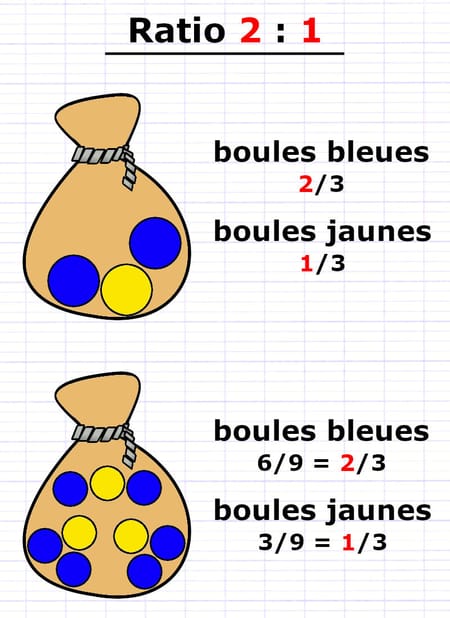
Le ratio 2 : 1 signifie qu’il y a 2/3 de boules bleues et 1/3 de boules jaunes.
Ratio 3 : 2 et 2 : 3
Le ratio 3 : 2 indique que le rapport entre deux grandeurs est de 3 pour 2. Dans un sac, des boules bleues et jaunes sont dans un ratio 3 : 2 s’il y a trois boules bleues pour deux boules jaunes. La proportion des boules de couleur peut s’écrire à l’aide d’une fraction :
- 3/5 des boules sont bleues.
- 2/5 des boules sont jaunes.
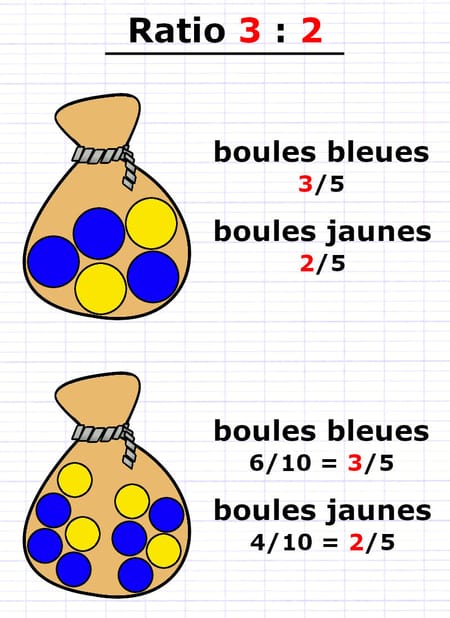
Les boules bleues et jaunes sont dans un ratio 3 : 2 dans chaque sac.
L’ordre des nombres au sein d’un ratio est très important. Si dans un sac, les boules bleues et jaunes sont dans un ratio 2 : 3, alors il y a deux boules bleues pour trois boules jaunes. La proportion des boules de couleur a été permutée :
- 2/5 des boules sont bleues.
- 3/5 des boules sont jaunes.
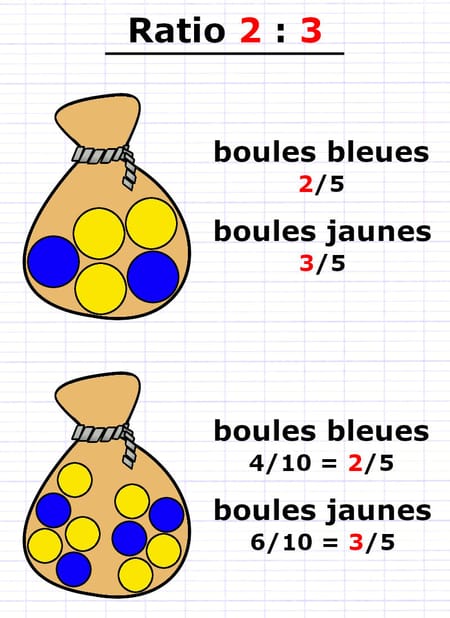
Les boules bleues et jaunes sont dans un ratio 2 : 3 dans chaque sac.
Ratio 3 : 2 : 1
Le ratio 3 : 2 : 1 indique que le rapport entre trois grandeurs est de 3 pour 2 pour 1. Dans un sac, des boules bleues, jaunes et rouges sont dans un ratio 3 : 2 : 1 s’il y a trois boules bleues pour deux boules jaunes et une boule rouge. Le ratio 3 : 2 : 1 indique donc qu’il y a trois fois plus de boules bleues (grandeur 1) que de boules rouges (grandeur 3), et deux fois plus de boules jaunes (grandeur 2) que de boules rouges (grandeur 3).
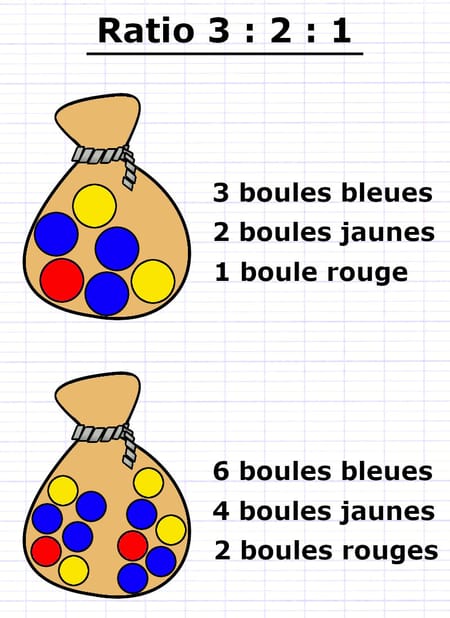
Les boules bleues, jaunes et rouges sont dans un ratio 3 : 2 : 1 dans chaque sac.
La proportion de chaque grandeur dans un ratio 3 : 2 : 1 peut s’écrire à l’aide d’une fraction :
- Le numérateur est l’un des nombres du ratio : 3 (grandeur 1), 2 (grandeur 2) ou 1 (grandeur 3).
- Le dénominateur est la somme des nombres du ratio : 6 (3 + 2 + 1).
Si les boules bleues, jaunes et rouges sont dans un ratio 3 : 2 : 1, alors :
- 3/6 (= 1/2) des boules sont bleues.
- 2/6 (= 1/3) des boules sont jaunes.
- 1/6 des boules sont rouges.
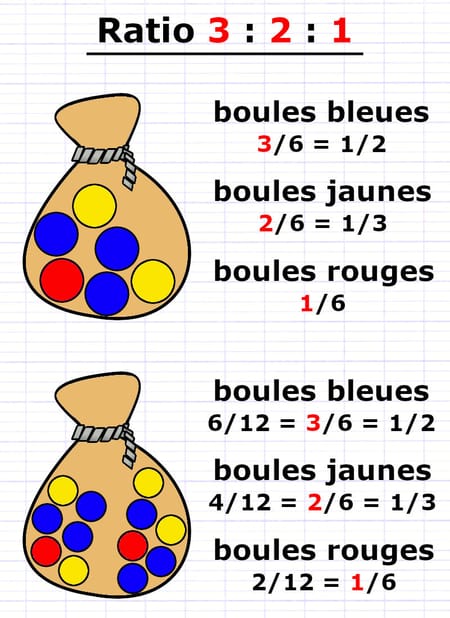
Le ratio 3 : 2 : 1 signifie qu’il y a 3/6 de boules bleues, 2/6 de boules jaunes et 1/6 de boules rouges.
Exercices
Question 2
Dans un sac, des boules bleues et jaunes sont respectivement dans un ratio de 3 : 1. Quelle fraction indique la proportion de boules jaunes dans le sac ?