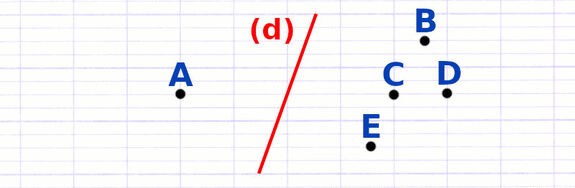
Construire l’Image d’un Point par Symétrie Axiale
Théorie
Dans une symétrie axiale, les constructions s’effectuent par rapport à une droite appelée axe de symétrie. L’image d’un point par symétrie axiale est le symétrique du point de l’autre côté de l’axe de symétrie.
Exemple

Comment construire l’image du point A par symétrie axiale d’axe (d) ? La droite (d) est l’axe de symétrie.
Tracer une Perpendiculaire
La 1re étape est de tracer la droite perpendiculaire à l’axe de symétrie qui passe par le point. La perpendiculaire forme un angle droit (90°) avec l’axe de symétrie.
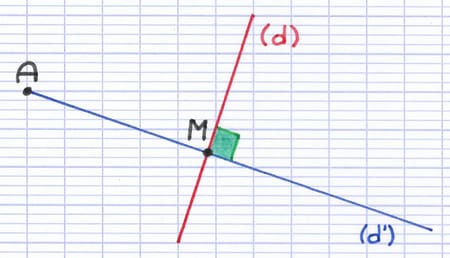
La droite (d’) est perpendiculaire à l’axe de symétrie (d) et passe par le point A. Le point M est le point d’intersection des 2 droites.
Mesurer la Distance
Grâce à la perpendiculaire, on peut mesurer facilement la distance entre le point et l’axe de symétrie. La distance correspond à la longueur du segment entre le point et l’intersection des 2 droites.
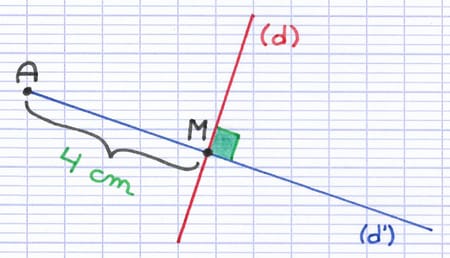
On mesure la distance entre le point et l’axe de symétrie en plaçant une règle graduée le long de la perpendiculaire. La distance est la longueur du segment [AM] : 4 cm.
Trouver le Symétrique du Point
2 points symétriques sont situés à égale distance d’un axe de symétrie. Le symétrique du point se trouve sur la perpendiculaire, de l’autre côté de l’axe de symétrie. Pour le trouver, on reporte la distance mesurée à l’étape 2 de l’autre côté de l’axe de symétrie.
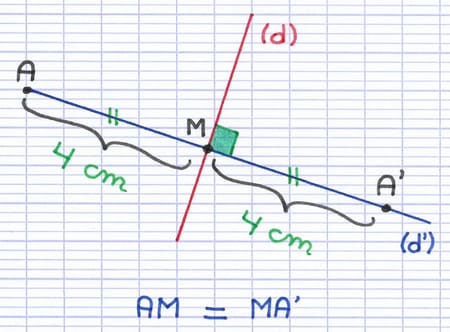
À partir du point d’intersection des 2 droites, on reporte la longueur AM de l’autre côté. A’ est le symétrique (l’image) du point A par symétrie axiale d’axe (d). L’axe de symétrie est situé à égale distance des 2 points symétriques.
Technique au compas
Il est également possible de trouver l’image (le symétrique) d’un point à l’aide d’un compas. Après avoir tracé la perpendiculaire (étape 1), on place la pointe du compas sur le point d’intersection des 2 droites. On trace alors un cercle passant par le point dont on souhaite construire le symétrique.
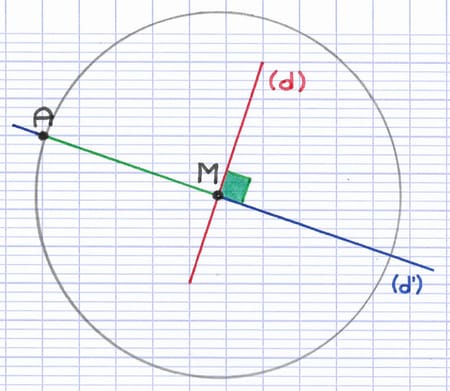
On peut trouver le symétrique du point A avec un cercle tracé au compas. Le point d’intersection des 2 droites (M) est le centre du cercle. Le cercle passe par le point A, son rayon est donc le segment [AM].
Le point d’intersection entre le cercle et la perpendiculaire, de l’autre côté de l’axe de symétrie, est le symétrique du point. Grâce à cette technique, il n’est pas nécessaire de mesurer la distance entre le point et l’axe de symétrie (étape 2) !
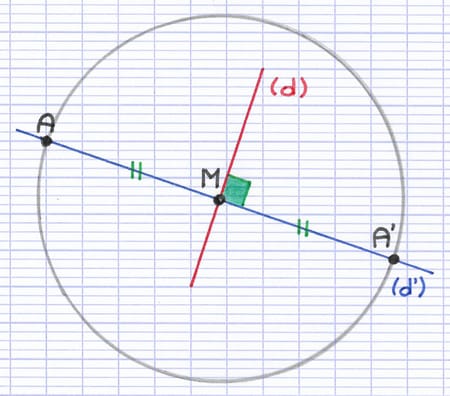
La construction au compas fait apparaître l’image du point. A’ est l’image (symétrique) du point A par symétrie axiale d’axe (d).