Construire le Tableau à Double Entrée d’Épreuves Successives
Théorie
Le tableau à double entrée permet de visualiser les issues d’une expérience aléatoire à deux épreuves successives. Chaque cellule du tableau met en relation une issue de la 1re épreuve avec une issue de la 2e épreuve.
Construction
Expérience : "On tire, deux fois de suite et avec remise, une boule dans une urne contenant 2 boules rouges, 1 boule verte et 1 boule jaune".
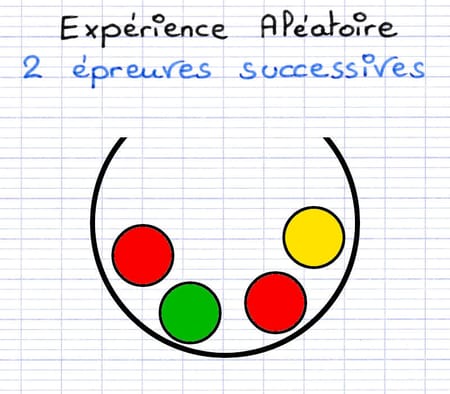
Comment construire le tableau à double entrée de ces 2 épreuves successives ?
Identifier les Épreuves Successives
Cette expérience aléatoire est composée de deux épreuves successives :
- La 1re épreuve correspond au 1er tirage d’une boule dans l’urne.
- La 2e épreuve correspond au 2e tirage d’une boule dans l’urne.
Ces deux épreuves sont identiques et indépendantes, car la boule obtenue au 1er tirage est remise dans l’urne avant de procéder au 2e tirage.
Tracer le Tableau à Double Entrée
La construction du tableau à double entrée s’articule autour de la 1re colonne et de la 1re ligne :
- La 1re colonne est composée des issues de la 1re épreuve.
- La 1re ligne est composée des issues de la 2e épreuve.
La case en haut à gauche du tableau est coupée en deux afin de donner un titre à la 1re colonne et la 1re ligne.
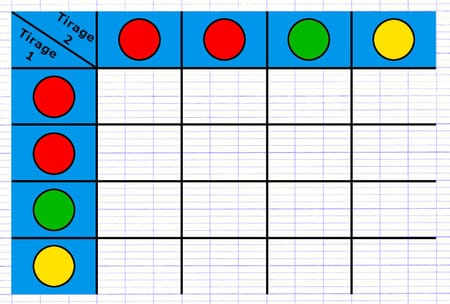
La 1re et 2e épreuve sont composées des quatre mêmes issues : 2 boules rouges, 1 boule verte et 1 boule jaune.
Il est également possible de placer les issues de la 1re épreuve dans la 1re ligne, et les issues de la 2e épreuve dans la 1re colonne.
Remplir le Tableau
L’étape suivante est de remplir toutes les cellules à l’intérieur du tableau à double entrée. Chaque cellule est la combinaison des issues de la 1re et 2e épreuve. Étant donné que chaque épreuve consiste à tirer une boule, la combinaison des deux épreuves est composée de 2 boules.
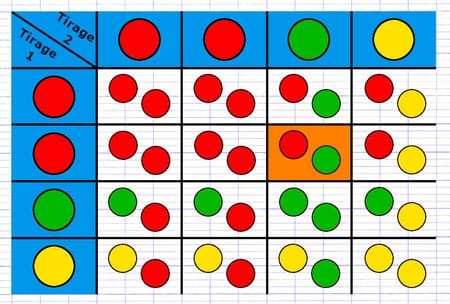
La case orange est la combinaison de 2 issues : tirer une boule rouge (1er tirage) et une boule verte (2e tirage).
Interpréter le Tableau
Le tableau à double entrée offre une vision d’ensemble des issues d’une expérience aléatoire à deux épreuves successives. Le nombre de cellules à l’intérieur du tableau indique le total des issues de l’expérience.
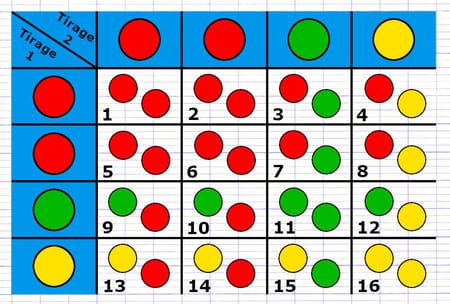
Cette expérience aléatoire à 2 épreuves successives possède 16 issues.
La probabilité d’un événement est une fraction dont :
- Le numérateur est le nombre d’issues de l’événement.
- Le dénominateur est le total des issues de l’expérience.
On peut donc calculer facilement la probabilité d’un événement en comptant les cases correspondant au sein du tableau.
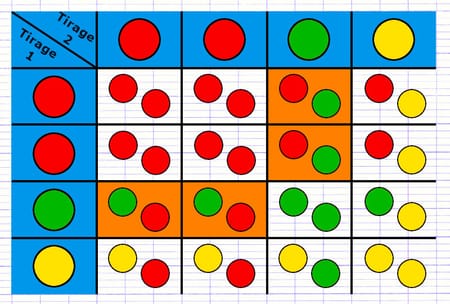
Il y a 4 issues correspondant à l’événement obtenir une boule rouge et une boule verte. La probabilité d’obtenir une boule rouge et verte est donc de 4/16 (= 1/4).
Quiz
Question 1
On lance deux fois de suite un dé à 6 faces, puis on note la somme des deux résultats obtenus. Quelle valeur faut-il insérer dans le tableau à double entrée, à l’intersection de la colonne 3 et de la ligne 4 ?
Question 2
On lance deux fois de suite un dé à 6 faces, puis on note la somme des deux résultats obtenus. Combien y a-t-il d’issues différentes au sein de cette expérience aléatoire ?
Question 3
On lance deux fois de suite un dé à 6 faces, puis on note la somme des deux résultats obtenus. Quelle est la probabilité d’obtenir la somme 9 ?