Mettre des Fractions sur un Dénominateur Commun
Théorie
Si on multiplie par un même nombre le numérateur et le dénominateur d’une fraction, alors on obtient une fraction égale à celle de départ. La multiplication transforme l’écriture de la fraction, mais les 2 fractions sont égales, car elles représentent la même proportion.
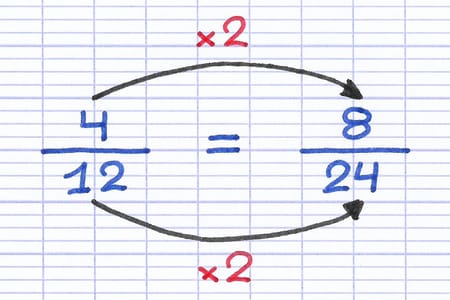
Le numérateur et le dénominateur de la fraction 4/12 sont multipliés par 2. Le résultat obtenu (8/24) est une fraction égale à celle de départ (4/12).
Cette propriété peut être utilisée pour transformer des fractions afin qu’elles partagent un dénominateur commun (identique). Mettre des fractions sur un dénominateur commun permet ensuite de les additionner, les soustraire ou les comparer facilement.
Exemple
Comment mettre les fractions 5/6 et 3/10 sur un dénominateur commun ?
1. Trouver le Dénominateur Commun
Le dénominateur commun est le plus petit commun multiple (PPCM) des dénominateurs. Pour trouver ce PPCM, on dresse par ordre croissant la liste des multiples de chaque dénominateur, et on sélectionne le plus petit multiple en commun.
Grâce à la liste des multiples de chaque dénominateur, on repère facilement le plus petit commun multiple (30) qui est le dénominateur commun.
2. Trouver la Multiplication au Dénominateur
On cherche ensuite le nombre par lequel multiplier le dénominateur de chaque fraction pour obtenir le dénominateur commun. Étant donné que le dénominateur commun est un multiple de chaque dénominateur, ce nombre ne devrait pas être difficile à trouver.
Pour la 1re fraction, on multiplie le dénominateur de départ (6) par 5 pour obtenir le dénominateur commun (30).
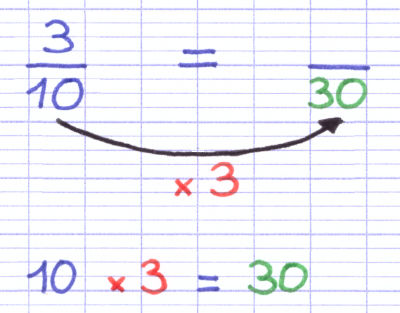
Pour la 2e fraction, on multiplie le dénominateur de départ (10) par 3 pour obtenir le dénominateur commun (30).
3. Multiplier chaque Numérateur
Le numérateur de chaque fraction est ensuite multiplié par le même nombre qu’au dénominateur. Le résultat de la multiplication est une fraction égale à la fraction de départ, car le numérateur et le dénominateur ont été multipliés par un nombre identique. Les fractions obtenues partagent désormais un dénominateur commun.
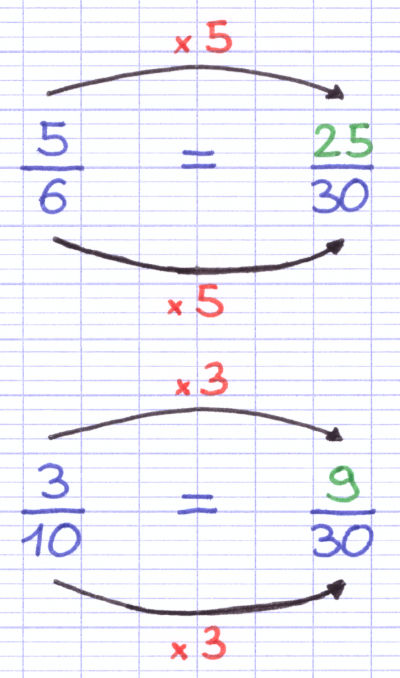
Pour la 1re fraction, comme le dénominateur a été multiplié par 5, on multiplie également le numérateur par 5. Pour la 2e fraction, comme le dénominateur a été multiplié par 3, on multiplie également le numérateur par 3. On obtient 2 fractions sur un dénominateur commun (25/30 et 9/30).
Exercices
Question 1
Quel est le plus petit dénominateur commun de ces deux fractions ?
Question 2
On souhaite que le dénominateur de cette fraction devienne 72. Par quel nombre faut-il multiplier le dénominateur et le numérateur ?
Question 3
On souhaite placer ces deux fractions sur leur plus petit dénominateur commun. Quelles fractions obtient-on ?