Placer un Point dans un Repère Orthogonal

🎯

Questions validées : 0 / 3

Théorie

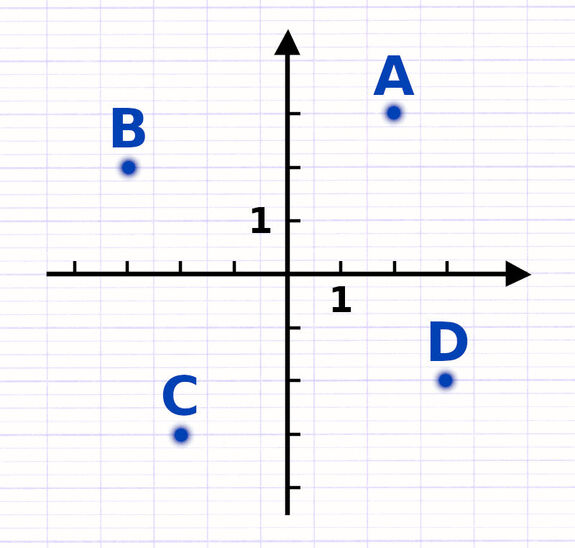
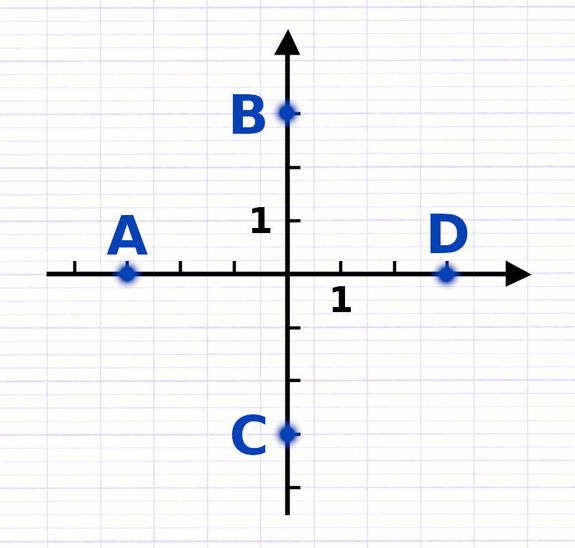
Un repère cartésien orthogonal est composé de 2 axes gradués perpendiculaires : l’axe des abscisses et l’axe des ordonnées. La graduation des axes permet de positionner des points au sein du repère.

★

Exemple

★

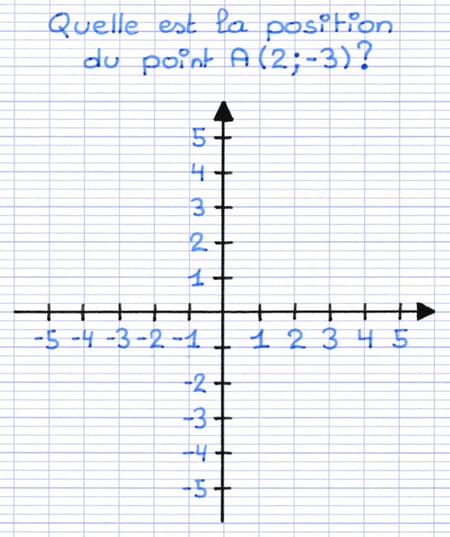
Placer un point dans un repère orthogonal — Comment placer le point A dans un **repère orthogonal** ?

1. Lire les Coordonnées du Point

Les coordonnées d’un point sont toujours constituées de deux nombres relatifs. Le point A est associé à deux nombres relatifs (2 et -3) qui sont ses coordonnées :

Le 1^er nombre (2) est l’abscisse : il indique la position sur l’axe horizontal.
Le 2^e nombre (-3) est l’ordonnée : il indique la position sur l’axe vertical.

Les coordonnées d’un point sont toujours notées entre parenthèses et séparées par un point-virgule : (2;-3).

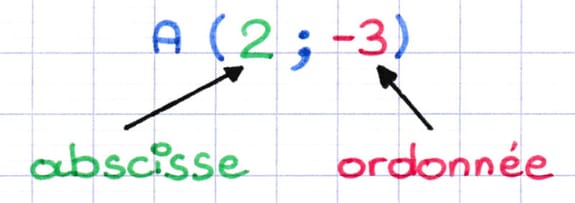
Coordonnées d’un point composées d’une abscisse et d’une ordonnée — Les **coordonnées** du point A sont (2;-3).

L’abscisse de A est 2 et l’ordonnée de A est -3.

2. Indiquer la Position en Abscisse

L’abscisse (2) indique la position du point par rapport à l’axe horizontal. Sur l’axe horizontal, on place une croix sur la graduation correspondante. Cette croix servira de repère pour placer le point (étape 4).

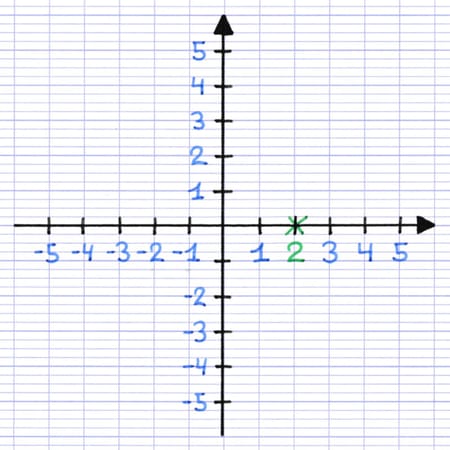
Position d’un point sur l’axe horizontal des abscisses — L’**abscisse** du point A est 2.

Une croix indique la position du point par rapport à l’axe horizontal.

3. Indiquer la Position en Ordonnée

L’ordonnée (-3) indique la position du point par rapport à l’axe vertical. Sur l’axe vertical, on place une croix sur la graduation correspondante. Cette croix servira de repère pour placer le point (étape 4).

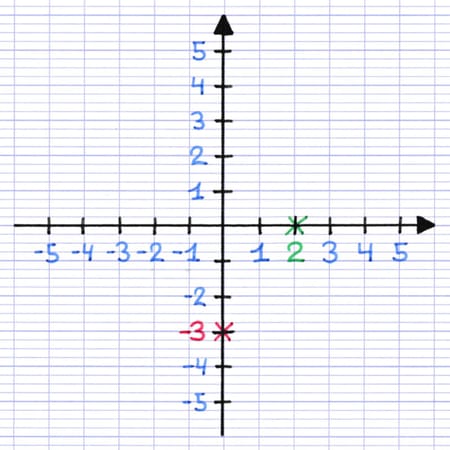
Position d’un point sur l’axe vertical des ordonnées — L’**ordonnée** du point A est -3.

Une croix indique la position du point par rapport à l’axe vertical.

4. Placer le Point dans le Repère

La dernière étape est de placer le point dans le repère cartésien en traçant deux droites perpendiculaires :

Une droite perpendiculaire à l’axe horizontal passant par l’abscisse (2).
Une droite perpendiculaire à l’axe vertical passant par l’ordonnée (-3).

Le point d’intersection des deux droites est la position du point A dans le repère.

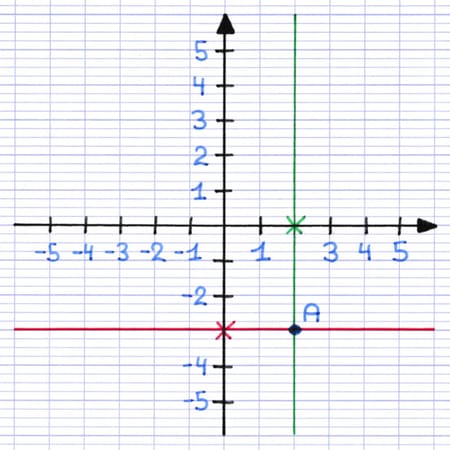
Point à l’intersection des 2 droites perpendiculaires — Tous les points sur la droite verte ont pour abscisse 2.

Tous les points sur la droite rouge ont pour ordonnée -3.

Le **point d’intersection** des deux droites est l’unique point de coordonnées (2;-3).

Lorsqu’on maîtrise la technique, il est possible d’effectuer toutes ces étapes mentalement. Il suffit d’imaginer les deux droites et de placer directement le point au niveau de leur intersection.