Reconnaître des Angles Alternes-Internes et Alternes-Externes
Théorie
Les angles alternes-internes et alternes-externes apparaissent lorsque 2 droites sont coupées par une sécante. Une sécante est une droite qui coupe une ou plusieurs autres droites.
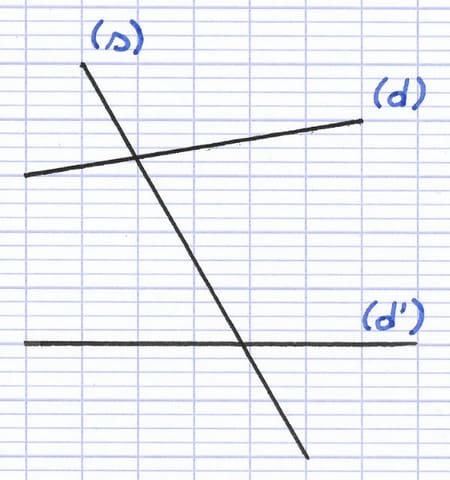
Les droites (d) et (d') sont coupées par une sécante (s). Les angles alternes-internes et alternes-externes apparaissent dans cette configuration.
Angles alternes-internes
2 angles alternes-internes sont reconnaissables à l’aide de 3 propriétés :
- Ils sont à l’intérieur de 2 droites coupées par une sécante (interne).
- Ils ne sont pas du même côté de la sécante (alterne).
- Leur sommet n’est pas identique.
2 droites coupées par une sécante forment 2 paires d’angles alternes-internes.
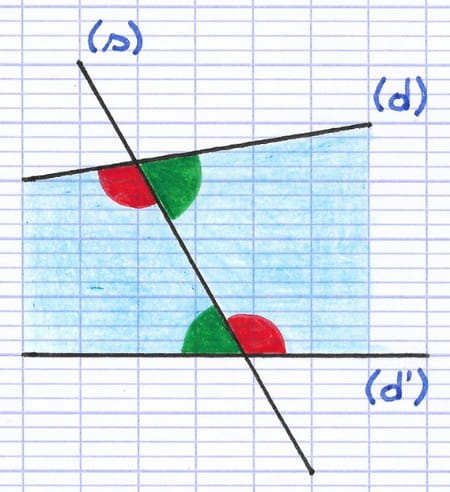
La zone bleue est l’intérieur des 2 droites coupées par la sécante.
Les 2 angles rouges sont alternes-internes : l’un est à gauche de la sécante, l’autre à droite.
Les 2 angles verts sont alternes-internes : l’un est à droite de la sécante, l’autre à gauche.
Angles alternes-externes
2 angles alternes-externes sont reconnaissables à l’aide de 3 propriétés :
- Ils sont à l’extérieur de 2 droites coupées par une sécante (externe).
- Ils ne sont pas du même côté de la sécante (alterne).
- Leur sommet n’est pas identique.
2 droites coupées par une sécante forment 2 paires d’angles alternes-externes.
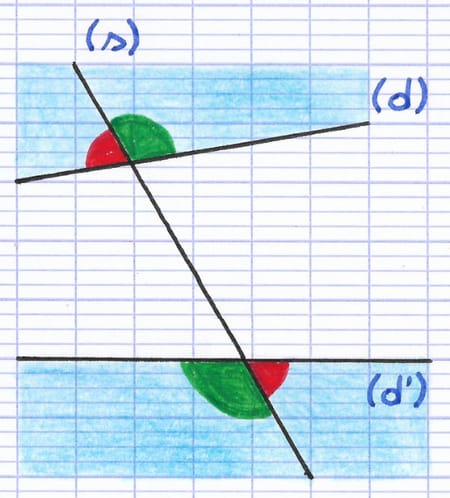
La zone bleue est l’extérieur des 2 droites coupées par la sécante.
Les 2 angles rouges sont alternes-externes : l’un est à gauche de la sécante, l’autre à droite.
Les 2 angles verts sont alternes-externes : l’un est à droite de la sécante, l’autre à gauche.
Exercices
Question 1
Laquelle de ces paires d’angles sont alternes-internes ?
Question 2
Combien de paire(s) d’angles alternes-externes sont formés lorsque deux droites sont coupées par une sécante ?
Question 3
Laquelle de ces paires d’angles sont alternes-externes ?