Reconnaître des Angles Opposés par le Sommet
Théorie
En géométrie, des angles opposés par le sommet ont la même mesure. 2 angles opposés par le sommet sont facilement reconnaissables à l’aide de 3 propriétés :
- Ils sont formés par 2 droites sécantes.
- Leur sommet est identique.
- Ils sont face à face (les côtés de l’un des angles sont le prolongement des côtés de l’autre angle).
Exemple
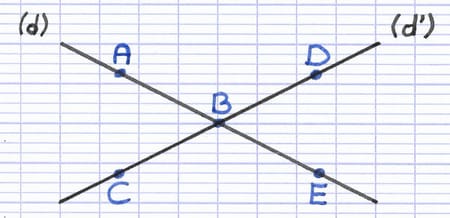
Comment reconnaître les angles opposés par le sommet de cette figure ?
Les points A, B et E appartiennent à la droite (d).
Les points C, B et D appartiennent à la droite (d').
1. Identifier 2 Droites Sécantes
La 1ère étape est de vérifier la présence de 2 droites sécantes. En effet, les angles opposés par le sommet sont toujours formés par 2 droites sécantes. 2 droites sont sécantes si elles ont un point d’intersection (point commun où les droites se croisent).
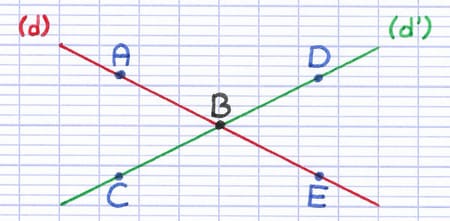
(d) et (d') sont 2 droites sécantes. B est le point d’intersection des 2 droites.
2. Identifier les Angles de Sommet Identique
On identifie ensuite les angles dont le sommet est identique. 2 droites sécantes forment 4 angles qui partagent le même sommet. Le sommet identique est le point d’intersection des 2 droites sécantes.
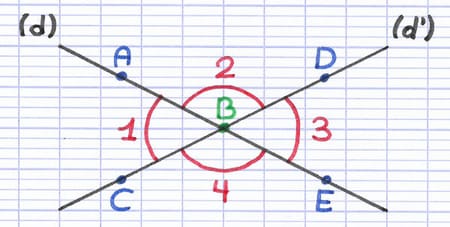
ABC, CBE, EBD et DBA sont 4 angles qui ont le même sommet. Leur sommet identique est le point B.
3. Identifier les Angles Face à Face
On peut désormais trouver facilement les angles opposés par le sommet en identifiant les angles face à face. 2 angles opposés par le sommet sont l’un en face de l’autre. Les côtés de l’un des angles sont le prolongement des côtés de l’autre angle. 2 droites sécantes forment 2 paires d’angles opposés par le sommet.
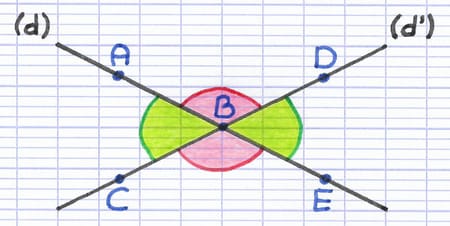
Les angles ABC et DBE sont face à face. Le côté [BE] de l’angle DBE est le prolongement du côté [AB] de l’angle ABC. Le côté [BD] de l’angle DBE est le prolongement du côté [CB] de l’angle ABC. Les angles ABC et DBE sont opposés par le sommet, ils ont la même mesure. Les angles ABD et CBE sont également opposés par le sommet.
Exercice
Question 1
Lesquels de ces angles sont des angles opposés par le sommet ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
Lequel de ces angles est opposé par le sommet à l’angle ABD ?