Reconnaître et Décrire un Polygone
Théorie
Un polygone est une ligne brisée fermée composée d’une suite de segments de droite :
- Si un (ou plusieurs) segment est courbé (arrondi), il ne s’agit pas d’un polygone.
- Si la ligne brisée n’est pas fermée, il ne se s’agit pas d’un polygone.
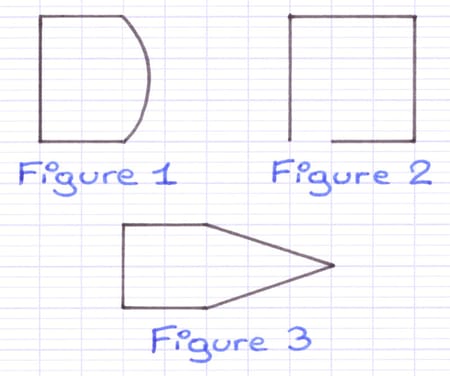
La figure 1 n’est pas un polygone, car l’un des segments est arrondi.
La figure 2 n’est pas un polygone, car la ligne brisée n’est pas fermée.
La figure 3 est un polygone, car la ligne brisée est fermée.
Un polygone est une figure géométrique plane limitée par des segments. En géométrie, une figure plane est une figure en 2D (2 dimensions).
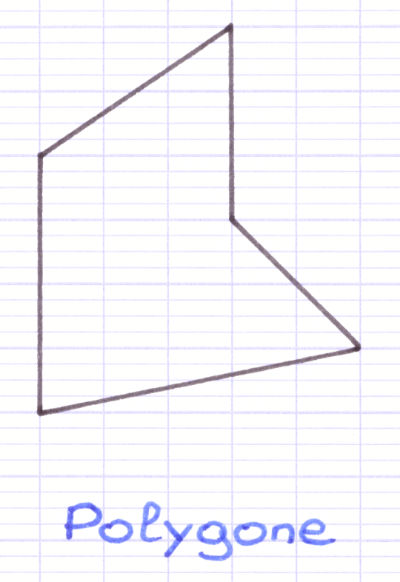
Un polygone est une figure géométrique plane.
Description
Sommets
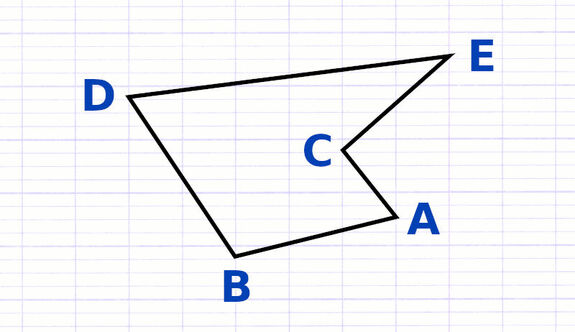
Les sommets du polygone correspondent aux différents coins de la figure. Le nom de chaque sommet est une lettre de l’alphabet en majuscule.
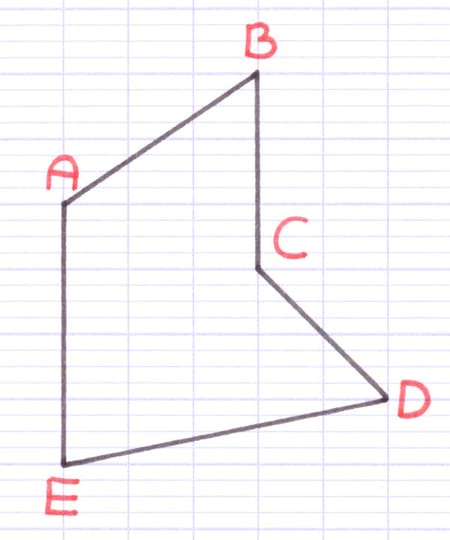
Ce polygone possède 5 sommets : A, B, C, D et E.
Nom
Le nom du polygone est composé de tous ses sommets rangés dans le sens horaire (sens des aiguilles d’une montre) ou anti-horaire. Il est possible de nommer un même polygone de différentes façons. Le nom du polygone varie en fonction du sens de rotation (horaire ou anti-horaire) et du sommet de départ.
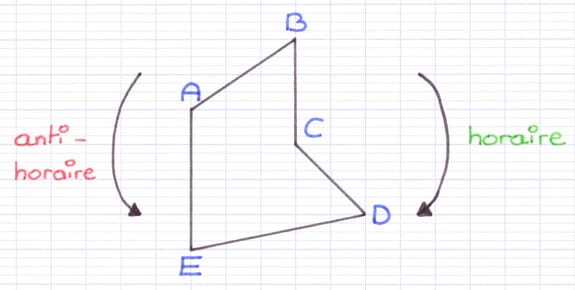
Quelques noms dans le sens horaire : ABCDE, CDEAB...
Quelques noms dans le sens anti-horaire : EDCBA, BAEDC...
Segments
Les segments du polygone correspondent aux différents côtés de la figure. Chaque segment est une ligne qui relie 2 sommets. Le nom des segments est composé des 2 sommets placés entre crochets (l’ordre des lettres n’a pas d’importance).
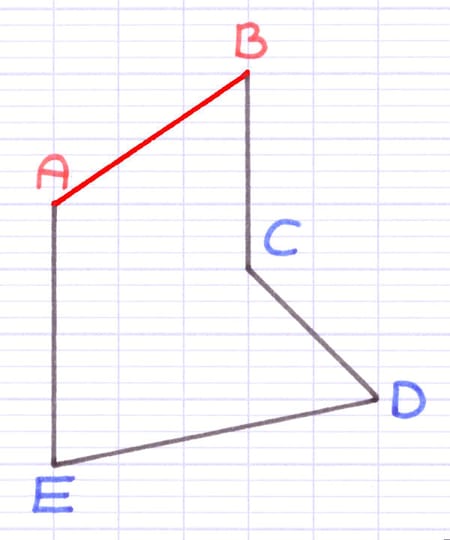
Ce polygone possède 5 segments : [AB], [BC], [CD], [DE], [EA].
Exercice
Question 1
Laquelle de ces figures n’est pas un polygone ?
Question 2
Quel nom peut-on donner à ce polygone ?
Question 3
Combien de nom(s) différent(s) peut-on donner à ce polygone ?