Reconnaître et Décrire un Solide Polyèdre
Théorie
Un solide est une figure géométrique en 3D (3 dimensions). Un solide est polyèdre si toutes ses faces sont des polygones (figures planes fermées par des segments de droite).
La caractéristique d’un solide polyèdre est que toutes ses faces sont des polygones.
Sommets
Les sommets du solide correspondent aux différents coins de la figure. Le nom du solide est composé de ses sommets rangés par ordre alphabétique.
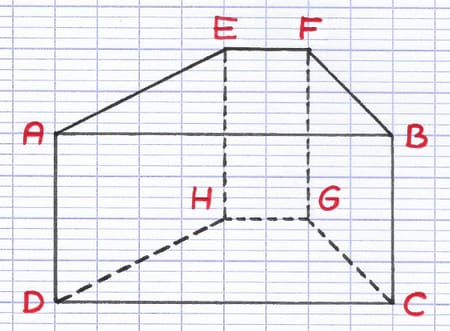
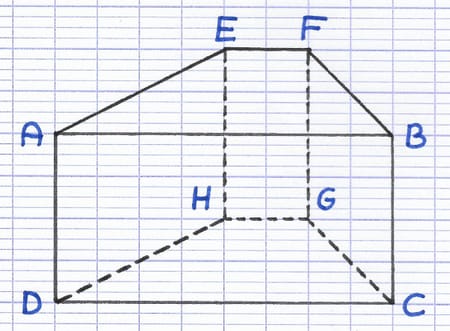
Ce solide polyèdre possède 8 sommets : A, B, C, D, E, F, G, H. Le nom du solide est ABCDEFGH.
Arêtes
Les arêtes du solide sont les segments qui relient ses sommets. Le nom des arêtes est composé des 2 sommets placés entre crochets.
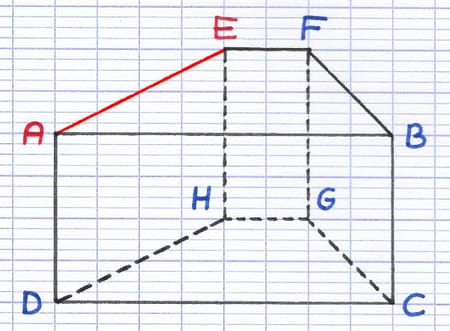
Le nom de l’arête en rouge est [AE] ou [EA]. Ce solide possède 12 arêtes : [AB], [BC], [CD], [DA], [EF], [FG], [GH], [HE], [AE], [DH], [FB], [GC].
Faces
Les faces du solide sont les surfaces planes (2D) délimitées par ses arêtes. Le nom des faces est composé de ses sommets rangés dans le sens des aiguilles d’une montre (ou dans le sens contraire).
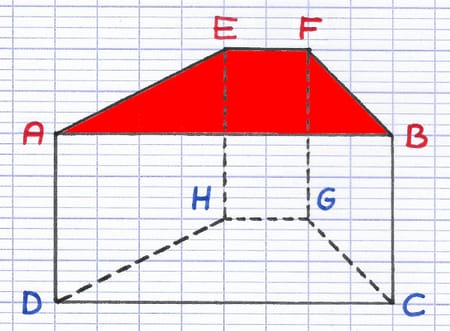
Le nom de la face en rouge est AEFB. Ce solide possède 6 faces : ABCD, EFGH, AEHD, FBCG, EFBA et HGCD.
Exercice
Question 1
Combien de sommets possède ce solide polyèdre ?
Question 2
Combien d’arêtes possède ce solide polyèdre ?
Question 3
Combien de faces possède ce solide polyèdre ?