Tracer l’Arbre de Probabilité d’Épreuves Successives
Théorie
L’arbre de probabilité (appelé également arbre des issues ou arbre des possibles) permet de visualiser les issues d’une expérience aléatoire. L’arbre est constitué de différentes branches qui représentent les issues possibles de l’expérience.
Exemple
Expérience : "On tire, deux fois de suite et avec remise, une boule dans une urne contenant 3 boules vertes et 2 boules rouges".
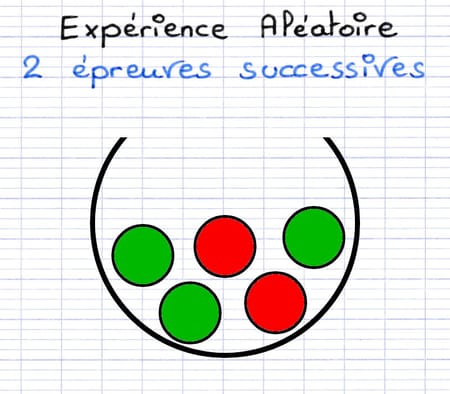
Comment tracer l’arbre de probabilité de ces 2 épreuves successives ?
1. Identifier les Épreuves Successives
Cette expérience aléatoire est composée de deux épreuves successives :
- La 1ère épreuve correspond au 1er tirage d’une boule dans l’urne.
- La 2ème épreuve correspond au 2ème tirage d’une boule dans l’urne.
Ces deux épreuves sont identiques et indépendantes, car la boule obtenue au 1er tirage est remise dans l’urne avant de procéder au 2ème tirage.
2. Tracer les Branches de la 1ère Épreuve
La construction de l’arbre de probabilité démarre en traçant une branche pour chaque issue de la 1ère épreuve. La 1ère épreuve de l’expérience aléatoire possède 2 issues (vert ou rouge) donc 2 branches. Une lettre majuscule désignant une des issues (V pour vert et R pour rouge) est ajoutée au bout de chaque branche.
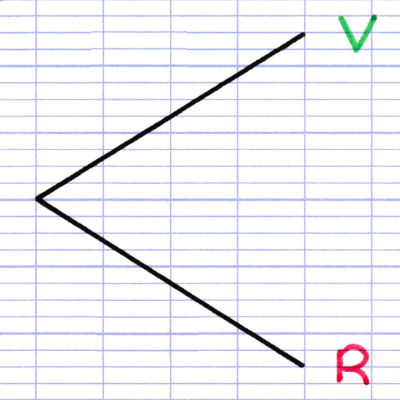
Chaque branche représente une issue de la 1ère épreuve de l’expérience aléatoire. Lors du 1er tirage, on peut obtenir une boule verte V ou rouge R.
3. Tracer les Branches de la 2ème Épreuve
À partir de chaque issue de la 1ère épreuve, on trace ensuite les branches correspondant aux issues de la 2ème épreuve. La 2ème épreuve de l’expérience aléatoire possède également 2 issues (vert et rouge) donc 2 branches. Une lettre majuscule désignant une des issues est ajoutée au bout de chaque nouvelle branche.
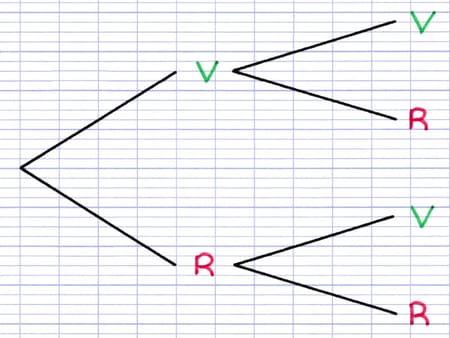
La 2ème épreuve démarre après avoir obtenu une boule verte ou rouge, il y a donc 2 points de départ différents. Lors du 2ème tirage, on peut également obtenir une boule verte V ou rouge R.
4. Indiquer les Issues Finales
On complète ensuite l’arbre des probabilités en indiquant les issues finales à l’extrémité des branches. Puisque l’expérience est composée de 2 tirages successifs, chaque issue finale est composée de 2 boules de couleur.
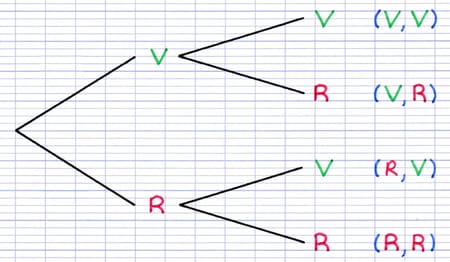
Cette expérience aléatoire à deux épreuves possède 4 issues finales : (V,V), (V,R), (R,V) et (R,R). L’issue (V, R) signifie qu’on a obtenu une boule verte, puis une boule rouge.
5. Pondérer l'Arbre de Probabilité
La pondération de l’arbre s’effectue en indiquant sur chaque branche la probabilité d’obtenir l’issue correspondante. La probabilité d’obtenir une boule de couleur s’obtient en divisant le nombre de boules de cette couleur par le nombre total de boules.
Il est possible d’écrire chaque probabilité sous la forme d’une fraction, d’un nombre décimal ou d’un pourcentage.
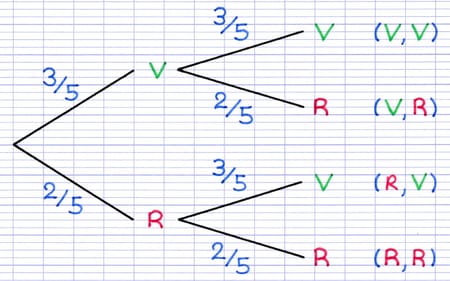
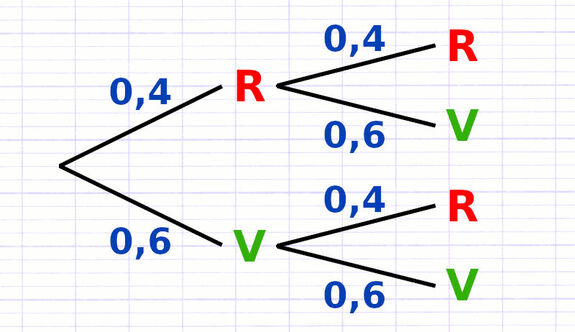
La pondération de l’arbre indique les probabilités des issues de chaque épreuve.
Il y a 3 boules vertes sur un total de 5 boules, la probabilité de tirer une boule verte est de 3/5 ou 0,6 ou 60%.
Il y a 2 boules rouges sur un total de 5 boules, la probabilité de tirer une boule rouge est de 2/5 ou 0,4 ou 40%.
Propriété : "La somme des probabilités des branches de même origine (point de départ identique) est toujours égale à 1".
Cette propriété peut être utilisée pour s’assurer que la pondération est correcte.
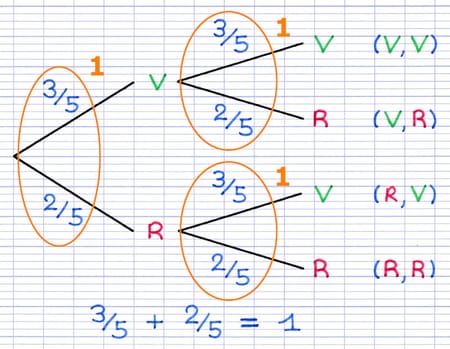
La somme des probabilités des branches de même origine est toujours égale à 1.
3/5 + 2/5 = 1
6. Calculer la Probabilité des Issues Finales
Pour compléter l’arbre de probabilité, on peut y ajouter la probabilité de chaque issue finale. Pour calculer la probabilité d’une issue finale, il suffit de multiplier les probabilités des branches menant à cette issue. La probabilité d’une issue finale se note à l’extrémité de sa branche.
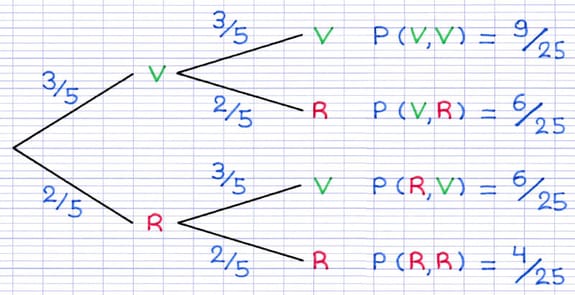
La probabilité d’une issue finale se calcule en multipliant les probabilités sur ses branches.
P(V,V) = 3/5 x 3/5 = 9/25
P(V,R) = 3/5 x 2/5 = 6/25
P(R,V)) = 2/5 x 3/5 = 6/25
P(R,R) = 2/5 x 2/5 = 4/25
Propriété : "La somme des probabilités des issues finales d’une expérience aléatoire est toujours égale à 1".
Cette propriété peut être utilisée pour s’assurer que les calculs sont corrects.
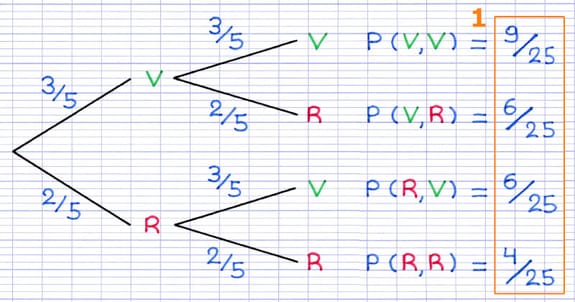
La somme des probabilités des issues finales d’une expérience aléatoire est toujours égale à 1.
9/25 + 6/25 + 6/25 + 4/25 = 25/25 = 1
Exercice
Question 1
On tire deux fois de suite et avec remise, une boule dans une urne contenant 6 boules bleues et 4 boules vertes. Quelle pondération doit-on placer sur la branche correspondant au tirage d’une boule bleue lors du 1er tirage ?
Question 2
Laquelle de ces propriétés est fausse ?
Question 3
Au sein de cet arbre de probabilité, R désigne la probabilité de tirer une boule rouge, tandis que V désigne la probabilité de tirer une boule verte. Quelle est la probabilité de tirer deux boules vertes successivement ?