Tracer un Repère Cartésien Orthogonal et Orthonormé
Théorie
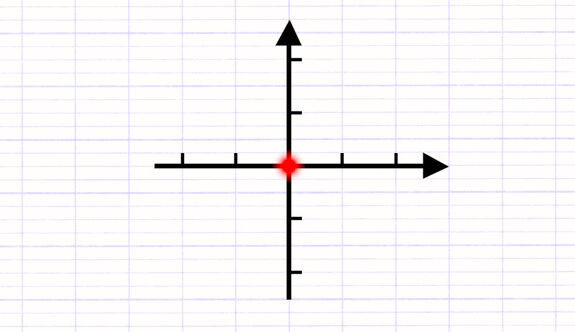
Un repère cartésien orthogonal est formé de 2 droites perpendiculaires :
- Une droite horizontale appelée l’axe des abscisses.
- Une droite verticale appelée l’axe des ordonnées.
Le point d’intersection des 2 droites est appelée l’origine du repère.
1. Tracer l’Axe des Abscisses
La 1re étape est de tracer l’axe des abscisses en traçant une droite horizontale orientée vers la droite. On place un petit trait au milieu de la droite afin de représenter l’origine du repère.
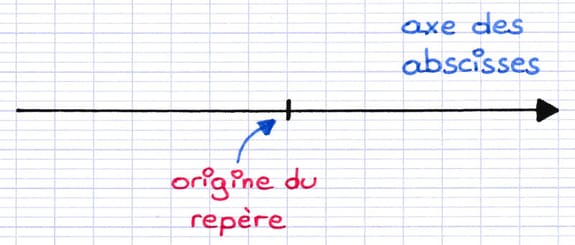
L’axe des abscisses est une droite horizontale orientée vers la droite.
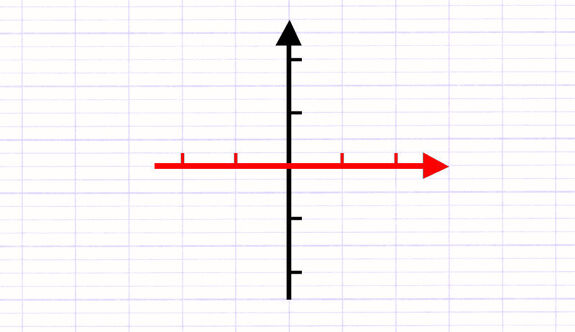
2. Tracer l’Axe des Ordonnées
On trace ensuite l’axe des ordonnées en traçant une droite verticale orientée vers le haut. Cette droite est perpendiculaire à l’axe des abscisses et passe par l’origine du repère. Le repère cartésien est dit orthogonal, car les deux axes sont perpendiculaires.
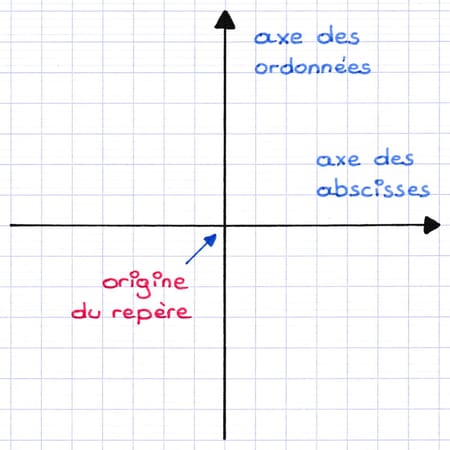
L’axe des ordonnées est une droite verticale orientée vers le haut.
3. Graduer le Repère Cartésien
On ajoute ensuite la graduation de chaque axe en partant de l’origine du repère qui vaut 0 :
- Sur l’abscisse, les nombres positifs sont à droite de l’origine, et les nombres négatifs à gauche.
- Sur l’ordonnée, les nombres positifs sont en haut de l’origine, et les nombres négatifs en bas.
L’échelle de graduation dépend de la longueur des axes et des valeurs à représenter. Le repère est dit orthonormé (ou orthonormal), car en plus de posséder des axes perpendiculaires, la graduation est identique sur chaque axe.
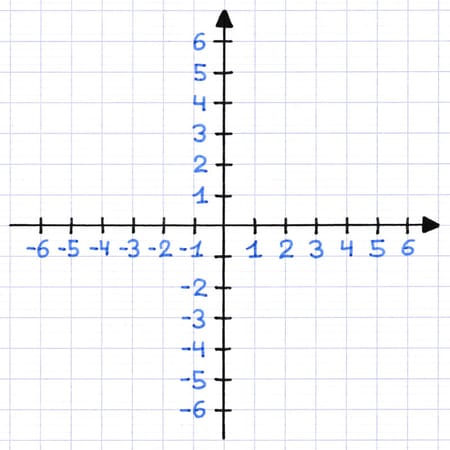
L’origine du repère vaut 0 sur l’axe des abscisses et des ordonnées. La graduation du repère cartésien s’effectue autour de cette origine.