Trouver l’Opposé d’un Nombre Relatif
Théorie
Les nombres relatifs désignent l’ensemble des nombres positifs (2, 7...) et négatifs (-3, -12...). 2 nombres relatifs sont opposés si :
- Leur valeur numérique (valeur absolue) est identique.
- Leur signe est différent (l’un est positif, l’autre est négatif).
3 et -3 sont des exemples de nombres opposés. Ils ont la même valeur numérique (3), mais leur signe est différent.
Pour trouver l’opposé d’un nombre, il suffit de transformer son signe :
- L’opposé d’un nombre positif est un nombre négatif.
- L’opposé d’un nombre négatif est un nombre positif.
À noter qu’il n’est pas obligatoire de noter le signe "+" devant un nombre positif.
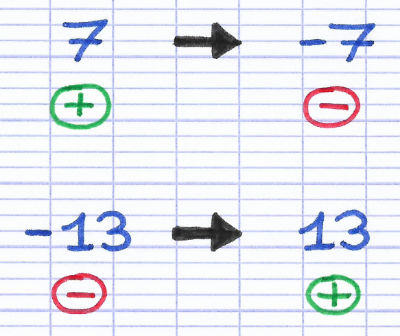
L’opposé de 7 (positif) est -7 (négatif).
L’opposé de -13 (négatif) est 13 (positif).
Propriété : "La somme de 2 nombres relatifs opposés est toujours égale à 0".
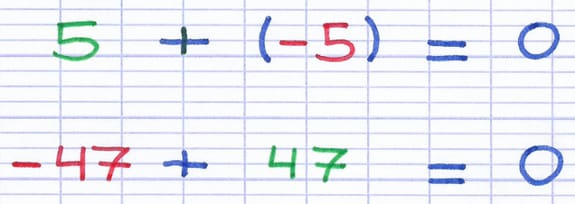
5 et -5 sont 2 nombres opposés, leur somme est égale à 0.
-47 et 47 sont 2 nombres opposés, leur somme est égale à 0.
Le chiffre 0 est considéré à la fois comme un chiffre positif et négatif. Zéro est donc un cas particulier, l’opposé de 0 est 0 !
L’opposé de 0 est 0.
Sur une droite graduée, deux nombres opposés sont à égale distance de 0. Le nombre négatif est à gauche de 0, tandis que le nombre positif est à droite de 0.
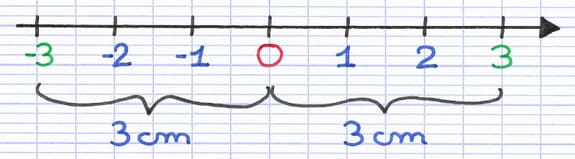
Sur cette droite graduée, les nombres opposés -3 et 3 sont à égale distance de 0.
Exercice
Question 1
Quel est l’opposé de 38 ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
Laquelle de ces propriétés est correcte ?