Utiliser la Règle de 3 pour Résoudre un Problème de Proportionnalité
Théorie
La règle de 3 permet de résoudre des problèmes où 2 nombres sont en situation de proportionnalité. 2 nombres sont en situation de proportionnalité s’ils évoluent dans les mêmes proportions (si l’un des nombres double, l’autre double également).
Exemple
Comment résoudre ce problème à l’aide de la règle de 3 ? La quantité d’ananas est proportionnelle au prix payé : si la quantité d’ananas double, le prix double également.
1. Établir une Relation de Proportionnalité
L’énoncé d’un problème de proportionnalité met en relation 2 nombres. La 1ère étape est d’établir une relation de proportionnalité en traçant une flèche horizontale entre les 2 nombres :
- On note à gauche le nombre qui subit une transformation dans l’énoncé.
- On note à droite le nombre dont il faudra calculer la transformation.
On trace une flèche horizontale entre la quantité d’ananas (9) et le prix (36). Le nombre d’ananas (9) est à gauche, car il est transformé dans l’énoncé (9 ananas devient 11 ananas). Le prix est à droite (36), car il faudra transformer ce nombre pour trouver le prix de 11 ananas.
2. Déduire une Relation de Proportionnalité avec 1
L’étape suivante est d’établir une nouvelle relation de proportionnalité en faisant apparaître le chiffre 1 à gauche. À partir de la relation de proportionnalité précédente :
- Le nombre à gauche est divisé par lui-même afin d’obtenir le chiffre 1.
- Le nombre à droite subit la même division afin de respecter la proportionnalité.
On obtient ainsi une relation de proportionnalité avec le chiffre 1.
Le nombre à gauche est divisé par lui-même pour obtenir le chiffre 1 (9 : 9 = 1). On effectue la même division à droite (36 : 9 = 4). On obtient ainsi le prix de 1 ananas.
3. Résoudre le Problème de Proportionnalité
Le problème peut maintenant être résolu en établissant une nouvelle relation de proportionnalité avec le nombre transformé à gauche. À partir de la relation de proportionnalité précédente :
- Le nombre à gauche (1) est multiplié par le nombre transformé afin d’obtenir le nombre transformé.
- Le nombre à droite subit la même multiplication afin de respecter la proportionnalité.
On obtient ainsi la relation de proportionnalité qui contient la solution au problème.
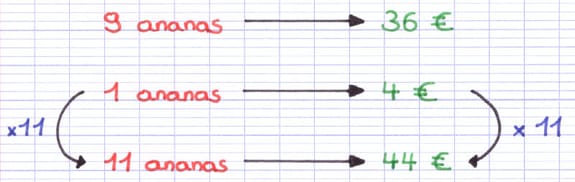
Dans l’énoncé, le nombre transformé est 11 (la quantité d’ananas passe de 9 à 11). Pour obtenir le nombre transformé à gauche, on multiplie le chiffre 1 par 11 (1 x 11 = 11). On effectue la même multiplication à droite (4 x 11 = 44). On obtient ainsi le prix de 11 ananas.
Astuce
La règle de 3 peut s’appliquer plus rapidement en effectuant simultanément la division (étape 2) et la multiplication (étape 3).
Le nombre à gauche est divisé par lui-même et la réponse est directement multipliée par le nombre transformé. Le nombre à droite subit les mêmes opérations afin de respecter le principe de proportionnalité. On obtient directement la réponse au problème.
Exercice
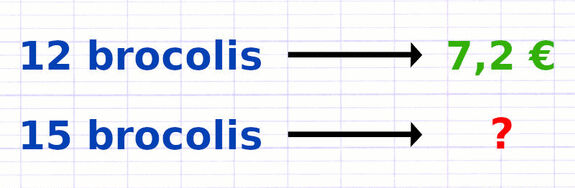
Question 1
Le prix des clémentines est proportionnel à la quantité achetée. Quel est le prix d’une clémentine ?
Question 2
Peut-on utiliser la règle de trois lorsque deux grandeurs ne sont pas en situation de proportionnalité ?
Question 3
Le prix des brocolis est proportionnel à la quantité achetée. Quel est le prix de 15 brocolis ?