Calculer les Longueurs, Angles et Aires de 2 Triangles

La figure ci-dessous n'est pas à l'échelle.

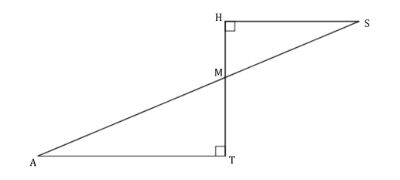
Les points M, A et S sont alignés.
Les points M, T et H sont alignés.
MH = 5 cm.
MS = 13 cm.
MT = 7 cm.

Vidéo de correction

Vidéo de correction de l'exercice

[HS] est le côté d'un triangle rectangle dont on connaît les 2 autres côtés. On peut donc démontrer que sa longueur est de 12 cm en utilisant le théorème de Pythagore.

Le théorème de Pythagore stipule que, dans un triangle rectangle, la longueur de l'hypoténuse au carré est égale à la somme des longueurs des 2 autres côtés au carré. L'hypoténuse est le côté qui est en face de l'angle droit. Dans cet exercice, l'hypoténuse est le côté [MS].

La démonstration s'effectue en commençant par mettre en équation le théorème de Pythagore: MS² = HM² + HS². Au sein de cette équation, MS peut être remplacé par 13 et HM par 5. En élevant ces deux valeurs au carré, on obtient: 169 = 25 + HS².

L'étape suivante consiste à isoler HS² au sein de l'équation afin d'obtenir HS² = 169 - 25. Le résultat de la soustraction est 144, ce qui signifie que HS² = 144. Or la racine carrée de 144 est égale à 12, donc la longueur HS est égale à 12 cm.

Les 2 triangles de l'exercice sont en situation de Thalès. En effet, ces 2 triangles sont formés par 2 droites sécantes, (HT) et (AS), ainsi que 2 droites parallèles, (HS) et (AT). On peut donc utiliser le théorème de Thalès pour calculer la longueur AT.

Les longueurs des côtés de 2 triangles en situation de Thalès sont proportionnelles. Cette situation de proportionnalité peut être mise en équation à l'aide d'une égalité entre 3 fractions. Le numérateur de chaque fraction correspond aux côtés d'un triangle, tandis que le dénominateur correspond aux côtés de l'autre triangle. 2 côtés alignés sont représentés au sein de la même fraction.

Après avoir établi l'égalité entre les 3 fractions, HM peut être remplacé par 5, MT par 7, MS par 13 et HS par 12. On peut donc affirmer que 5/7 = 12/AT. En effectuant le produit en croix, on obtient que 5 x AT = 7 x 12. En résolvant cette équation on trouve que AT = 16,8. La longueur AT mesure donc 16,8 cm.

L'angle HMS se situe au sein d'un triangle rectangle. On peut donc utiliser les relations trigonométriques pour trouver la mesure de cet angle. D'après les formules de trigonométrie, le cosinus de HMS est égal à la longueur du côté adjacent sur la longueur de l'hypoténuse. Autrement dit, cos HMS = 5/13.

À partir de cette formule, on utilise la fonction arccos ou cosinus inverse de la calculatrice pour déterminer la mesure de HMS. Il est important de vérifier que la calculatrice se trouve en mode degré, et non en mode radian. La réponse obtenue est d'environ 67, donc l'angle HMS mesure approximativement 67 degrés.

Parmi les propositions, on retrouve la symétrie centrale, la symétrie axiale, la rotation, la translation et l'homothétie. Ces 4 premières transformations ont la particularité de conserver la mesure des longueurs. Pourtant les longueurs du triangle MHS sont différentes du triangles MAT !

Cela signifie qu'il ne peut pas s'agir de l'une de ces 4 premières transformations. La transformation qui permet d'obtenir le triangle MAT à partir du triangle MHS est donc l'homothétie. Il s'agit d'une homothétie de centre M et de rapport -1.

La longueur MT est 1,4 fois plus grande que la longueur HM. Cela ne signifie toutefois pas que l'aire du triangle MAT est 1,4 fois plus grande que l'aire du triangle MHS !

Lors d'un agrandissement de rapport k, les longueurs sont multipliées par k, mais les aires sont multipliées par k², et les volumes par k³. Donc si les longueurs sont multipliées par 1,4, les aires sont multipliées par 1,4², soit 1,96.

L'affirmation de l'élève est donc fausse. L'aire du triangle MAT est 1,96 fois plus grande que l'aire du triangle MHS.

Exercice en image

Cet exercice est extrait de l'épreuve de mathématiques du Brevet des Collèges (DNB) Amérique du Nord (3 juin 2022).