Calculer une Probabilité avec un Dé Équilibré à 20 Faces
Énoncé
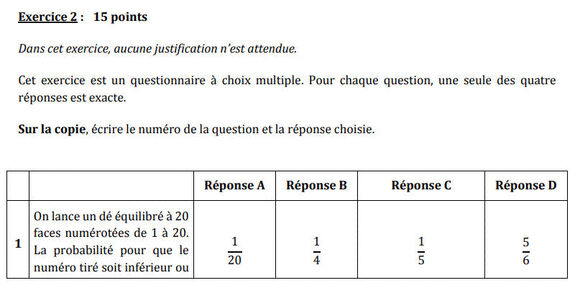
On lance un dé équilibré à 20 faces numérotées de 1 à 20.
Question 1
La probabilité pour que le numéro tiré soit inférieur ou égal à 5 est :
Correction
Situation d’équiprobabilité
Cet exercice de probabilité implique un dé équilibré à 20 faces numérotées de 1 à 20. Que le dé soit équilibré signifie qu’il n’est pas truqué. La probabilité de tomber sur n’importe quelle face est identique.
L’exercice consiste à déterminer la probabilité d’obtenir un numéro inférieur ou égal à 5 en lançant le dé. Il s’agit d’une situation d’équiprobabilité, car les issues de cette expérience aléatoire sont équiprobables. La probabilité d’obtenir n’importe quel nombre est identique.
Probabilité d’un événement
« Obtenir un numéro inférieur ou égal à 5 » est un événement aléatoire. La probabilité d’un tel événement en situation d’équiprobabilité est une fraction. Le numérateur correspond au nombre d’issues de l’événement. Le dénominateur est le nombre d’issues total de l’expérience aléatoire.
L’événement « obtenir un numéro inférieur ou égal à 5 » possède cinq issues (les cinq faces numérotées de 1 à 5). Le nombre d’issues total de l’expérience aléatoire est 20 (les vingt faces du dé). La probabilité de l’événement est donc 5/20.
Par simplification, on obtient la fraction irréductible 1/4. Il y a donc 1 chance sur 4 d’obtenir un numéro inférieur ou égal à 5 en lançant ce dé.
Brevet
Cet exercice est extrait de l’épreuve de mathématiques du Diplôme National du Brevet (DNB) qui évalue les acquis de fin de Collège.
Série : Générale
Localisation : Amérique du Nord
Date : 3 juin 2022
Référence : Exercice 2
