Calculer le Volume Occupé par des Truffes dans des Boîtes

Pour fêter les 25 ans de sa boutique, un chocolatier souhaite offrir aux premiers clients de la journée une boîte contenant des truffes au chocolat.

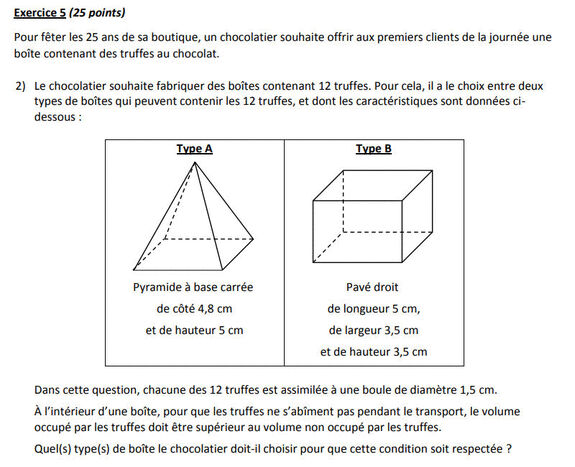
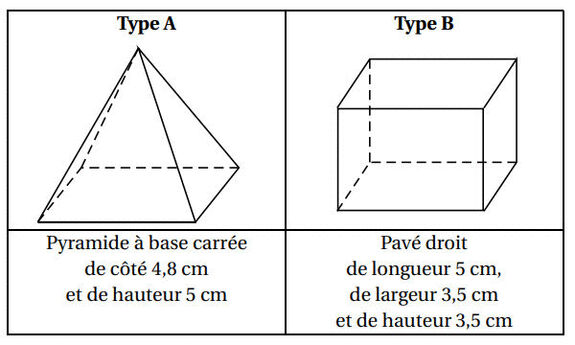
Le chocolatier souhaite fabriquer des boîtes contenant 12 truffes. Pour cela, il a le choix entre deux types de boites qui peuvent contenir les 12 truffes, et dont les caractéristiques sont données ci-dessous:

Dans cette question, chacune des 12 truffes est assimilée à une boule de diamètre 1,5 cm.

À l'intérieur d'une boîte, pour que les truffes ne s'abîment pas pendant le transport, le volume occupé par les truffes doit être supérieur au volume non occupé par les truffes.

Rappels:

Le volume d'une boule de rayon r est: 4/3 x π x r³
Le volume d'une pyramide est: (aire de la base x hauteur) / 3
Le volume d'un pavé droit est: longueur x largeur x hauteur

Vidéo de correction

Vidéo de correction de l'exercice

Chaque truffe est est une boule d'un diamètre de 1,5 centimètres. La formule pour calculer le volume d'une boule est la suivante: 4/3 x π x Rayon³. Pour utiliser cette formule, il faut donc déterminer le rayon d'une truffe.

Le rayon est la moitié du diamètre. Le rayon d'une truffe est donc de 0,75 cm (1,5 : 2). Le volume d'une truffe est obtenu à l'aide du calcul suivant: 4/3 x x π x 0,75³. Le résultat arrondi au centième près est 1,77 cm³.

La première question consiste à calculer le volume de 12 truffes. 1,77 x 12 = 21,24. Le volume des 12 truffes est donc de 21,24 cm³.

La boîte A est en forme de pyramide. Le volume d'une pyramide est calculé en multipliant l'aire de sa base par sa hauteur, puis en divisant le résultat par 3. Cette pyramide possède une base carrée dont l'aire s'obtient en élevant la longueur d'un côté au carré.

La base est un carré de côté 4,8 cm. En élevant cette valeur au carré, on obtient 23,04 cm². La hauteur de la pyramide est de 5 cm. On multiplie donc ensuite l'aire obtenue par 5, puis on divise le résultat par 3. La réponse obtenue est le volume de la boîte A: 38,4 cm³.

La boîte B est un pavé droit (ou parallélépipède rectangle). Le volume d'un pavé droit est calculé en multipliant sa longueur, sa largeur et sa hauteur. 5 x 3,5 x 3,5 = 61,25. Le volume de la boîte B est donc de 61,25 cm³.

Pour obtenir le volume de l'espace vide au sein de la boîte A, on calcule la différence entre le volume de la boîte A (38,4 cm³) et le volume de toutes les truffes (21,24 cm³). 38,4 - 21,24 = 17,16. Le volume de l'espace vide dans la boîte A est donc de 17,16 cm³.

On constate que le volume des 12 truffes est bien supérieur au volume de l'espace non occupé. Cela signifie donc que la boîte A peut convenir pour le chocolatier.

Pour obtenir le volume de l'espace vide au sein de la boîte B, on calcule la différence entre le volume de la boîte B (61,25 cm³) et le volume de toutes les truffes (21,24 cm³). 61,25 - 21,24 = 40,01 Le volume de l'espace vide dans la boîte B est donc de 40,01 cm³.

On constate que le volume des 12 truffes est inférieur au volume de l'espace non occupé. Cela signifie donc que la boîte B ne peut pas convenir pour le chocolatier.

Exercice en image

Cet exercice est extrait de l'épreuve de mathématiques du Brevet des Collèges (DNB) Centres Étrangers (14 juin 2022).