Utiliser un Programme de Calcul avec des Nombres Entiers

On considère le programme de calcul suivant, appliqué à des nombres entiers:

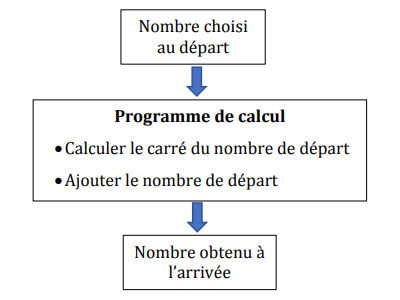
Question 1 / 6

Vérifier que si le nombre de départ est 15, alors le nombre obtenu à l'arrivée est 240.

15 x 2 + 15 = 240 15² + 15² = 240 15² x 15 = 240 15² + 15 = 240

Question 2 / 6

Voici un tableau de valeurs réalisé à l'aide d'un tableur:

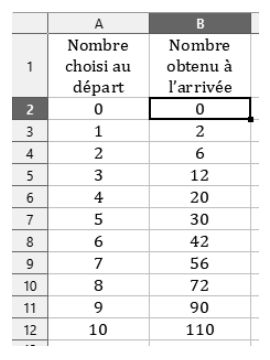
Il donne les résultats obtenus par le programme de calcul en fonction de quelques valeurs du nombre choisi au départ. Quelle formule a pu être saisie dans la cellule B2 avant d'être étirée vers le bas ?

= A2^2 + A2 B2 = A2^2 + A2 = A2*2 + A2 A2^2 + A2

Question 3 / 6

On note x le nombre de départ. Écrire, en fonction de x, une expression du résultat obtenu avec ce programme de calcul.

x² * x 2x + x x² + x 3x

Question 4 / 6

On considère l'affirmation suivante: "Pour obtenir le résultat du programme de calcul, il suffit de multiplier le nombre de départ par le nombre entier qui suit."

Vérifier que cette affirmation est vraie lorsque le nombre entier choisi au départ est 9.

9 x 10 = 90 et 9² + 9 = 90 9 x 8 = 72 et 9² - 9 = 72 9 + 8 = 17 et 17 - 8 = 9 9 + 10 = 19 et 19 - 10 = 9

Question 5 / 6

On considère l'affirmation suivante: "Pour obtenir le résultat du programme de calcul, il suffit de multiplier le nombre de départ par le nombre entier qui suit."

Démontrer que cette affirmation est vraie quel que soit le nombre entier choisi au départ.

x + (x + 1) = x² + x x + x + 1 = 2x + 1 x * (x + 1) = x² + x x * (x - 1) = x² - x

Question 6 / 6

Démontrer que le nombre obtenu à l'arrivée par le programme de calcul est un nombre pair quel que soit le nombre entier choisi au départ.

Le nombre de départ est élevé au carré, donc le résultat est toujours pair x * (x + 1) est la multiplication d'un nombre pair par un nombre impair dont le résultat est toujours pair En choisissant 15 comme nombre de départ, on obtient un nombre pair (240) x² + x est l'addition d'un nombre pair avec un nombre impair dont le résultat est toujours pair

Précédent

Suivant

Vous n'avez pas répondu à toutes les questions

Vidéo de correction

Vidéo de correction de l'exercice

La première question est de vérifier que si le nombre de départ et 15, alors le nombre obtenu à l'arrivée est 240. Pour effectuer cette vérification, il faut appliquer le programme de calcul en choisissant 15 comme nombre de départ.

La première étape du programme est de calculer le carré du nombre de départ. Le carré de 15 est égal à 225. Ensuite, l'étape suivante est d'y ajouter le nombre de départ. La somme de 225 et de 15 est 240. Le nombre obtenu à l'arrivée est donc 240.

Le tableur est constitué de différentes valeurs. La première colonne contient les nombres choisis au départ, tandis que la deuxième colonne regroupe les nombres obtenus à l'arrivée. La cellule B2 contient le nombre obtenu à l'arrivée lorsque le nombre au départ est celui de la cellule A2.

La formule de la cellule B2 correspond au programme de calcul appliqué à la cellule A2. Pour l'obtenir, le nombre de la cellule A2 est d'abord élevé au carré, puis on lui ajoute la valeur de la cellule A2. On obtient ainsi la formule = A2^2 + A2. Le signe d'égalité au début indique le début de la formule. L'accent circonflexe suivi du chiffre 2 indique qu'on élève la cellule A2 au carré.

On souhaite écrire en fonction de x une expression du résultat obtenu avec le programme de calcul. Cette expression peut être facilement obtenue en remplaçant le nombre de départ par l'inconnue x.

Puisque la première étape est de calculer le carré du nombre de départ, on obtient x². Ensuite, ajouter le nombre de départ signifie qu'on ajoute x. On obtient donc l'expression x² + x. Il s'agit de l'expression du résultat obtenu avec ce programme de calcul en fonction de x.

On affirme que "Pour obtenir le résultat du programme de calcul, il suffit de multiplier le nombre de départ par le nombre entier qui suit." Il faut vérifier que cette affirmation est vraie lorsque le nombre entier choisi au départ est 9. Pour cela, il suffit d'effectuer l'opération proposée et de vérifier que la réponse obtenue est la même que celle obtenue avec le programme de calcul.

Multiplier le nombre de départ par le nombre entier qui suit équivaut à multiplier 9 par 10 (10 est le nombre entier qui suit 9). Le résultat est 90. En appliquant le programme de calcul à 9, on obtient également 90 (9² + 9 = 81 + 9 = 90). L'affirmation est donc vraie lorsque le nombre de départ est 9.

On souhaite ensuite démontrer que l'affirmation précédente et vraie quel que soit le nombre entier choisi au départ. Cette démonstration s'effectue en choisissant x comme nombre de départ, car x peut représenter n'importe quel nombre entier.

On sait déjà que l'expression x² + x représente le nombre obtenu en fonction de x. En utilisant également x pour représenter le nombre obtenu selon l'affirmation, on obtient x(x + 1). En effectuant la distributivité simple, on obtient x² + x, la même expression que celle du programme de calcul ! Cela démontrer que l'opération décrite au sein de l'affirmation est identique à celle du programme de calcul.

La dernière question consiste à démontrer que le nombre obtenu à l'arrivée est un nombre pair, quel que soit le nombre entier choisi au départ. Puisque la démonstration concerne n'importe quel nombre entier choisi au départ, il faut également utiliser x pour représenter le nombre entier choisi au départ.

Pour cela, le plus simple est de partir de l'expression x(x+1). Cette expression représente la multiplication d'un nombre entier par le nombre entier qui le suit. On aura donc toujours un nombre pair multiplié par un nombre impair. Or le résultat d'une telle multiplication est toujours pair ! Donc le nombre obtenu à l'arrivée est toujours pair.

Exercice en image

Cet exercice est extrait de l'épreuve de mathématiques du Brevet des Collèges (DNB) Amérique du Nord (3 juin 2022).