Scratch : Utiliser un Programme de Dessin de Motif Aléatoire
Exercice
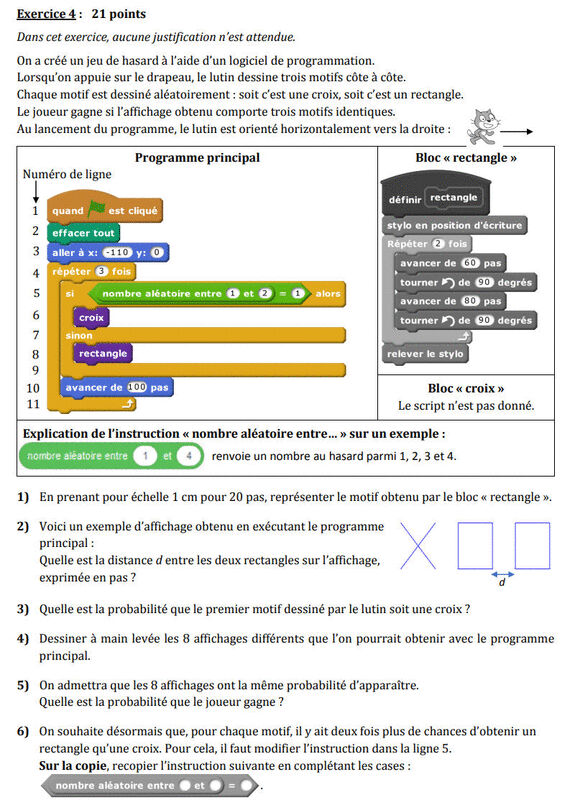
On a créé un jeu de hasard à l’aide d’un logiciel de programmation. Lorsqu’on appuie sur le drapeau, le lutin dessine trois motifs côte à côte. Chaque motif est dessiné aléatoirement : soit c’est une croix, soit c’est un rectangle. Le joueur gagne si l’affichage obtenu comporte trois motifs identiques. Au lancement du programme, le lutin est orienté horizontalement vers la droite.
Question 1
En prenant pour échelle 1 cm pour 20 pas, représenter le motif obtenu par le bloc « rectangle ».
Question 2
Voici un exemple d’affichage obtenu en exécutant le programme principal :
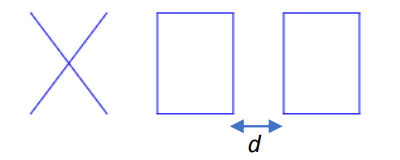
Quelle est la distance d entre les deux rectangles sur l’affichage, exprimée en pas ?
Question 3
Quelle est la probabilité que le premier motif dessiné par le lutin soit une croix ?
Question 4
Dessiner à main levée les 8 affichages différents que l’on pourrait obtenir avec le programme principal.
Question 5
On admettra que les 8 affichages ont la même probabilité d’apparaître. Quelle est la probabilité que le joueur gagne ?
Question 6
On souhaite désormais que, pour chaque motif, il y ait deux fois plus de chances d’obtenir un rectangle qu’une croix. Pour cela, il faut modifier l’instruction dans la ligne 5. Quelle est la nouvelle instruction ?
Correction
Représentation du motif du bloc rectangle
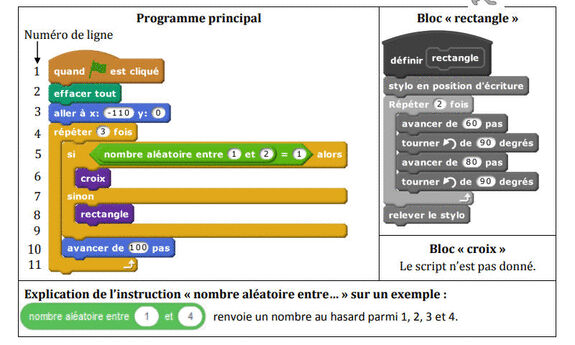
Le bloc rectangle de ce programme Scratch permet de tracer un rectangle. Le motif est obtenu en parcourant une boucle répétée deux fois. Les instructions de la boucle sont d’avancer de 60 pas, tourner dans le sens anti-horloger de 90°, avancer de 80 pas et tourner dans le sens anti-horloger de 90°.
Une fois la boucle répétée deux fois, on obtient un rectangle de dimension 80 pas sur 60 pas. À l’échelle de 1 cm sur 20 pas, cela représente un rectangle de 4 cm de longueur et 3 cm de largeur. Pour obtenir ces dimensions en centimètre, il suffit de diviser le nombre de pas par 20.
Distance entre deux rectangles
Pour déterminer la distance d entre les deux rectangles, il faut bien analyser le programme principal. On peut remarquer qu’on avance de 100 pas entre l’exécution des blocs croix et rectangle. Cela signifie que l’on se déplace de 100 pas entre les motifs, donc entre les rectangles.
Cette distance ne correspond toutefois pas à la distance d car, lorsqu’un rectangle est tracé, on se situe en bas à gauche de la figure. Lorsqu’on avance de 100 pas, on parcourt donc d’abord la largeur du rectangle correspondant à 60 pas. L’écart entre les deux rectangles est donc de 40, car « 100 - 60 = 40 ».
Probabilité du premier motif
La boucle du programme principal démarre en choisissant au hasard un nombre entre 1 et 2. Si le nombre est 1, le bloc « croix » est exécuté, sinon c’est le bloc « rectangle » qui est exécuté. Le choix du premier motif est donc aléatoire.
Il y a une chance sur deux d’obtenir le chiffre 1 lorsqu’on choisit un nombre aléatoire entre 1 et 2. Il y a donc une chance sur deux que le premier motif dessiné par le lutin soit une croix. La probabilité est donc de 1/2.
Différents affichages du programme
Il est possible d’obtenir huit affichages différents à partir du programme principal. En effet, le programme permet de dessiner trois motifs. Chaque motif est représenté sous la forme d’une croix ou d’un rectangle. Il y a donc deux possibilités par motif.
Les huit affichages différents sont les suivants :
- croix - croix - croix
- croix - croix - rectangle
- croix - rectangle - croix
- rectangle - croix - croix
- croix - rectangle - rectangle
- rectangle - croix - rectangle
- rectangle - rectangle - croix
- rectangle - rectangle - rectangle
Probabilité de gagner
Dans cet exercice, le joueur gagne si les trois motifs obtenus sont identiques. Le joueur peut donc gagner s’il obtient trois rectangles ou trois croix. Tous les autres affichages sont perdants, car ils ne comportent pas trois motifs identiques.
Il y a deux affichages qui font gagner le joueur, sur un total de huit affichages différents. La probabilité de gagner est donc de 2/8, autrement dit 1/4. Le joueur a une chance sur quatre de gagner.
Deux fois plus de chance d’obtenir un rectangle
On souhaite modifier l’instruction dans la ligne 5 pour qu’il y ait deux fois plus de chances d’obtenir un rectangle qu’une croix. La probabilité d’obtenir un rectangle ou une croix dépend du nombre choisi au hasard.
Pour qu’il y ait deux fois plus de chance d’obtenir un rectangle, on ajoute un chiffre à la liste des nombres choisis au hasard et on l’associe à l’exécution du bloc rectangle. De cette façon, il y a désormais deux chiffres permettant d’obtenir un rectangle, contre un seul chiffre permettant d’obtenir une croix. La nouvelle instruction doit donc être la suivante : « nombre aléatoire entre 1 et 3 = 1 ».
Extrait
Cet exercice est extrait de l’épreuve de mathématiques du Brevet Amérique du Nord (DNB) du 3 juin 2022.