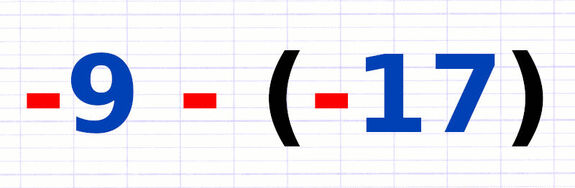
Additionner et Soustraire des Nombres Relatifs
Théorie
L’addition et la soustraction des nombres relatifs s’effectue en jonglant entre les signes positifs et négatifs. Il est donc important de maîtriser la règle des signes avant de s’aventurer à additionner et soustraire des nombres relatifs.
Exemple
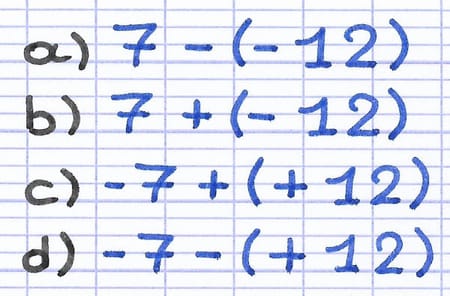
Comment effectuer l’addition et la soustraction de ces nombres relatifs ?
1. Appliquer la Règle des Signes
La 1re étape est d’observer chaque calcul à la recherche de 2 signes l’un à côté de l’autre. À chaque fois que 2 signes se suivent, on les fusionne en appliquant la règle des signes. Grâce aux transformations effectuées en appliquant la règle des signes, les calculs deviennent plus clairs.
- et - se transforment en +.
+ et - se transforment en -.
+ et + se transforment en +.
- et + se transforment en -.
L’étape suivante est différente selon le signe des nombres relatifs
2. Signes Identiques
2 nombres relatifs ont des signes identiques s’ils sont tous les deux positifs (+) ou négatifs (-). Dans ce cas, le signe du résultat de l’addition ou de la soustraction est toujours le même que le signe des 2 nombres.
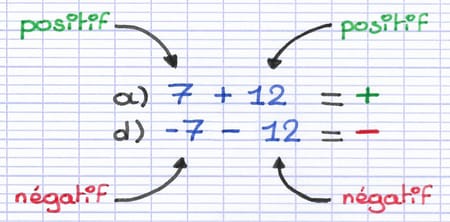
Dans le 1er calcul, les 2 nombres relatifs sont positifs, la réponse est donc positive.
Dans le 2e calcul, les 2 nombres relatifs sont négatifs, la réponse est donc négative.
Maintenant que l’on connaît le signe de la réponse, il ne reste plus qu’à calculer sa valeur. Pour cela, on effectue simplement la somme des 2 nombres relatifs, sans prendre en compte leur signe.
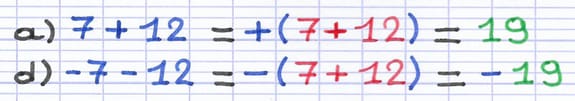
L’addition des deux nombres donne 19.
La 1re réponse est positive.
La 2e réponse est négative.
3. Signes Différents
2 nombres relatifs ont des signes différents si l’un est positif (+) et l’autre négatif (-). Dans ce cas, le signe du résultat de l’addition ou de la soustraction est le signe du plus grand nombre. Pour déterminer le plus grand nombre, on ne prend pas en compte leur signe.
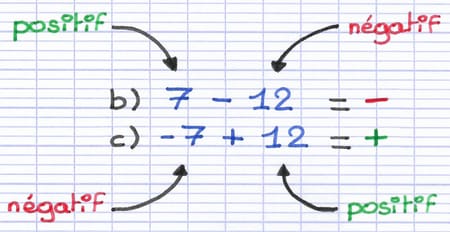
Sans prendre en compte leur signe, 12 est plus grand que 7. Au sein des deux calculs, le signe de la réponse est donc le signe de 12.
Maintenant que l’on connaît le signe de la réponse, il ne reste plus qu’à calculer sa valeur. Pour cela, on soustrait au plus grand nombre la valeur du plus petit nombre, sans prendre en compte leur signe.
Les deux nombres relatifs sans leur signe sont 7 et 12. La soustraction du plus grand par le plus petit donne 5.
La 1re réponse est négative.
La 2e réponse est positive.
Exercices
Question 1
Que devient cette expression lorsqu’on applique la règle des signes ?
Question 2
Quel est le résultat de ce calcul ?
Question 3
Quel est le résultat de ce calcul ?