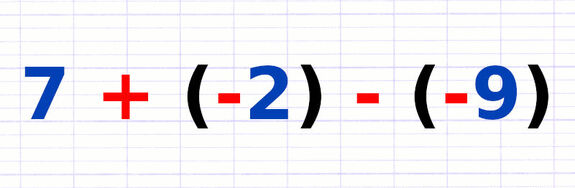Appliquer la Règle des Signes
Théorie
La règle des signes permet de résoudre des calculs où des signes positifs (+) et négatifs (-) sont mélangés. Cette règle détermine comment deux signes fusionnent ensemble pour ne former qu’un.
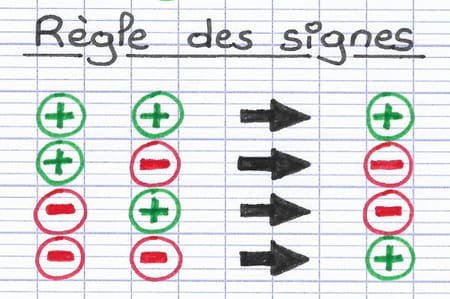
2 signes positifs se transforment en 1 signe positif.
1 signe positif et 1 signe négatif se transforment en 1 signe négatif.
1 signe négatif et 1 signe positif se transforment en 1 signe négatif.
2 signes négatifs se transforment en 1 signe positif.
La règle des signes s’applique principalement dans 2 situations :
- Lorsque des signes positifs (+) ou négatifs (-) se succèdent.
- Lorsqu’on multiplie ou divise des nombres relatifs (positifs ou négatifs).
Application de la Règle
Signes Successifs
Certains calculs sont composés de signes positifs (+) et négatifs (-) l’un à côté de l’autre. Lorsque 2 signes se suivent, ils fusionnent ensemble en respectant la règle des signes.
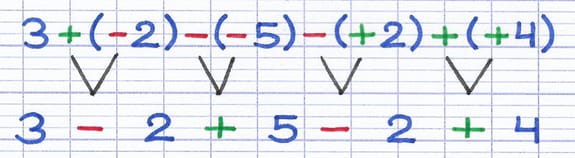
Des signes se suivent s’ils ne sont pas séparés par des nombres ou des lettres. Dans cet exemple, il y a 4 paires de signes qui fusionnent ensemble.
On procède ensuite à la résolution du calcul en respectant la priorité des opérations.
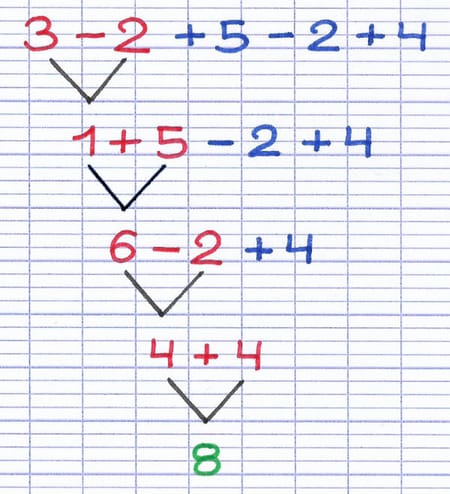
Les additions et soustractions sont effectuées de gauche à droite.
Multiplication et Division de Nombres Relatifs
Les nombres relatifs sont des nombres qui peuvent être positifs ou négatifs. Chaque multiplication et division de nombres relatifs s’effectue en respectant la règle des signes.
Un nombre négatif multiplié par un nombre positif donne un nombre négatif. Un nombre négatif divisé par un nombre négatif donne un nombre positif. Un nombre position multiplié par un nombre négatif donne un nombre négatif.
Technique de mémorisation
Pour mémoriser la règle des signes, on peut considérer le signe "+" comme un ami et le signe "-" comme un ennemi :
- L’ami de mon ami est mon ami (+ et + donne +).
- L’ami de mon ennemi est mon ennemi (+ et - donne -).
- L’ennemi de mon ami est mon ennemi (- et + donne -).
- L’ennemi de mon ennemi est mon ami (- et - donne +).
Exercices
Question 1
Quel est le résultat de ce calcul ?
Question 2
Quel est le signe final de cette expression si l’on applique la règle des signes ?
Question 3
Quel est le résultat de ce calcul ?