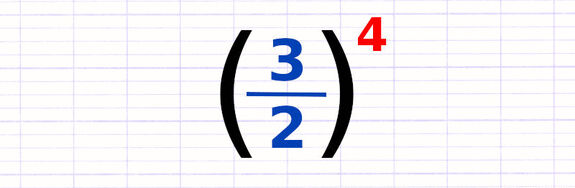
Appliquer les Propriétés des Puissances
Théorie
Chaque puissance (23) est composée de 2 éléments :
- Une base (2) qui indique le nombre à multiplier par lui-même.
- Un exposant (3) qui indique combien de fois la base est multipliée par elle-même.
Les propriétés des puissances sont des règles de calcul qui s’appliquent aux puissances. Chaque propriété est illustrée par une formule facile à mémoriser.
Formules illustrant les propriétés des puissances.
Produit de Puissances de Même Base
Propriété : "Le produit de puissances de même base s’effectue en additionnant les exposants".
Cette propriété permet de multiplier des puissances dont la base est identique.
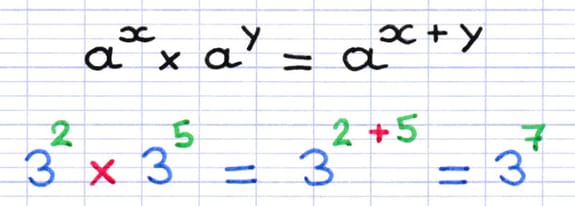
Formule et exemple illustrant le produit de puissances de même base.
Quotient de Puissances de Même Base
Propriété : "Le quotient de puissances de même base s’effectue en soustrayant les exposants".
Cette propriété permet de diviser des puissances dont la base est identique.
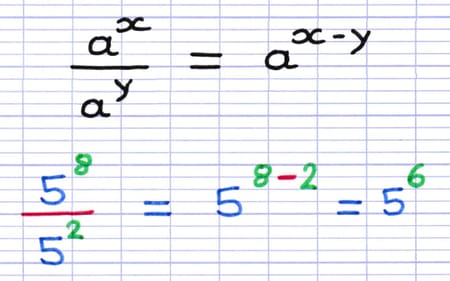
Formule et exemple illustrant le quotient de puissances de même base.
Puissance d'une Puissance
Propriété : "La puissance d’une puissance s’effectue en multipliant les exposants".
Cette propriété permet de calculer une puissance dont la base est une autre puissance.
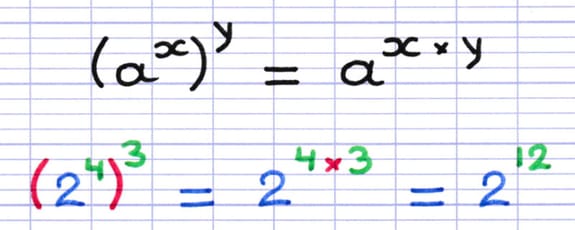
Formule et exemple illustrant la puissance d’une puissance.
Puissance d'une Multiplication
Propriété : "La puissance d'une multiplication s'effectue en distribuant la puissance à chaque facteur".
Cette propriété permet de calculer une puissance dont la base est un produit.
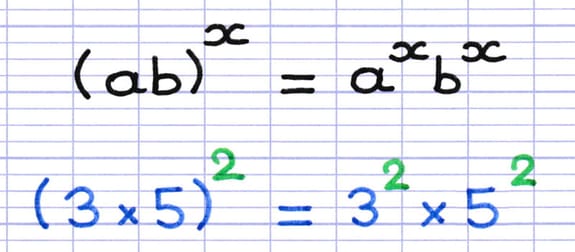
Formule et exemple illustrant la puissance d’une multiplication.
Puissance d'une Fraction
Propriété : "La puissance d’une fraction s’effectue en distribuant la puissance au numérateur et au dénominateur".
Cette propriété permet de calculer une puissance dont la base est une fraction.
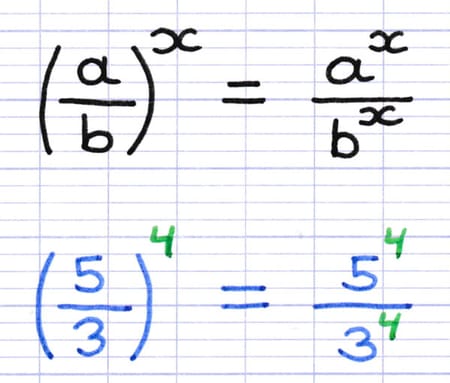
Formule et exemple illustrant la puissance d'une fraction.
Exercice
Question 1
Quel est le résultat de ce produit ?
Question 2
Quel est le résultat de ce calcul ?
Question 3
Que devient cette expression si on retire la parenthèse ?