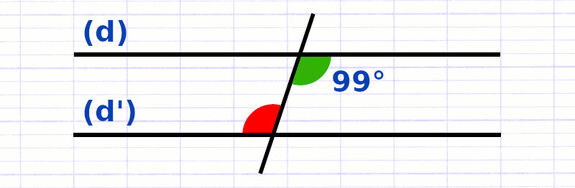
Associer Droites Parallèles et Angles alternes-internes
La propriété de parallélisme des angles alternes-internes et alternes-externes permet de déterminer si:
- 2 droites sont parallèles.
- 2 angles alternes-internes ou alternes-externes sont égaux.
Avant d'utiliser cette propriété, assure-toi d'être capable d'identifier des angles alternes-internes et alternes-externes.
Reconnaître des angles alternes-internes et alternes-externes
-
1
Identifier des droites parallèles
Propriété: Si 2 angles alternes-internes ou alternes-externes sont égaux (mesure identique), alors leurs droites sont parallèles.
Grâce à cette propriété, on peut démontrer le parallélisme de 2 droites.
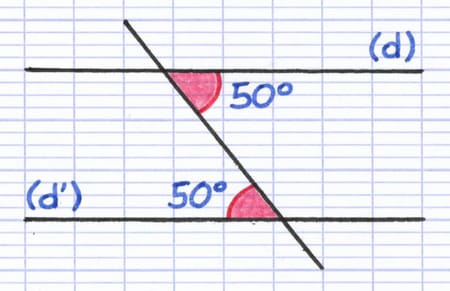
Les angles alternes-internes sont égaux, ils mesurent 50°.Les droites (d) et (d') sont donc parallèles.
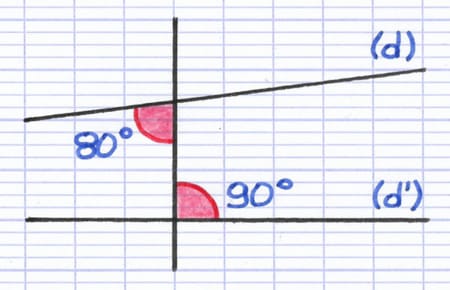
Les angles alternes-internes ont des mesures différentes.Les droites (d) et (d') ne sont donc pas parallèles. -
2
Identifier des angles alternes-internes et alternes-externes égaux
La même propriété peut s'utiliser dans l'autre sens pour déterminer si 2 angles alternes-internes ou alternes-externes sont égaux.
Propriété: Si 2 droites sont parallèles, alors leurs angles alternes-internes (ou alternes-externes) sont égaux.
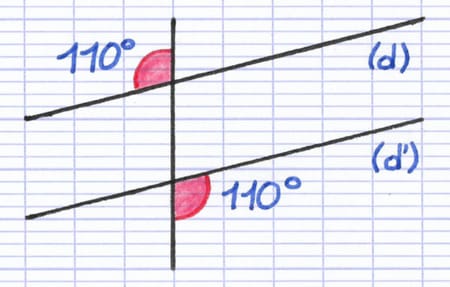
Les droites (d) et (d') sont parallèles.Les angles alternes-externes sont donc égaux (110°).
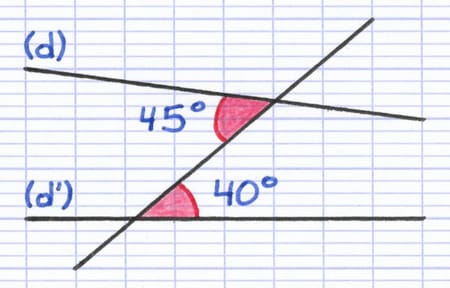
Les droites (d) et (d') ne sont pas parallèles.Les angles alternes-internes sont donc différents (45° et 40°).
Vérifiez si votre puissance mathématique a augmenté !
Déterminez la mesure de l'angle vert en justifiant votre réponse, puis comparez votre réponse avec la correction.
