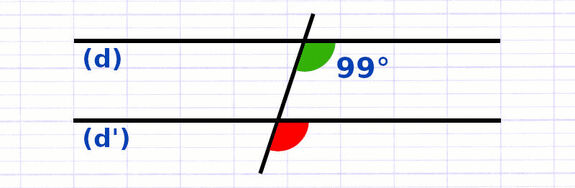
Associer Droites Parallèles et Angles Correspondants
Théorie
Les angles correspondants apparaissent quand une sécante coupe 2 droites. Grâce à la propriété de parallélisme des angles correspondants, on peut démontrer que :
- 2 angles correspondants sont égaux.
- 2 droites sont parallèles.
Angles Correspondants Égaux
Si 2 droites sont parallèles, alors leurs angles correspondants sont égaux. Des angles égaux sont des angles qui ont exactement la même mesure.
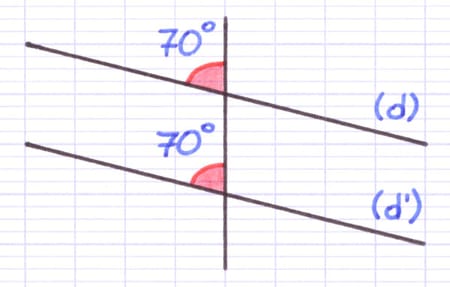
(d) et (d') sont 2 droites parallèles. Les angles correspondants sont donc égaux (70°).
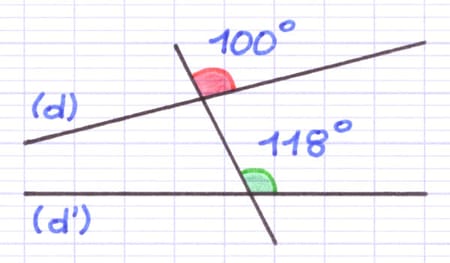
(d) et (d') sont 2 droites qui ne sont pas parallèles. Les angles correspondants sont donc différents (100° et 118°).
Droites Parallèles
On peut utiliser la même propriété à l’envers afin de démontrer le parallélisme de 2 droites. Si 2 angles correspondants sont égaux, alors leurs droites sont parallèles.
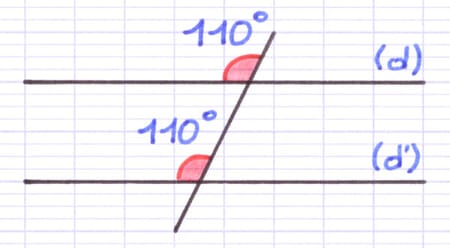
Les angles correspondants ont la même mesure (110°), ils sont égaux. (d) et (d') sont donc 2 droites parallèles.
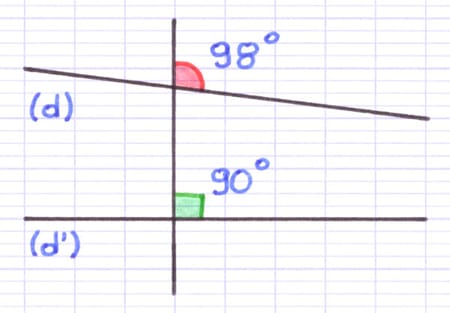
Les angles correspondants sont différents (98° et 90°). Les droites (d) et (d') ne sont donc pas parallèles.
Exercice
Question 1
Les droites (d) et (d’) étant parallèles, quelle est la mesure de l’angle en rouge ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
La propriété de parallélisme des angles correspondants permet de déterminer que :