Calculer la Moyenne Simple d’une Série Statistique
Théorie
Une série statistique est une suite de valeurs dont on peut calculer la moyenne :
- On calcule une moyenne simple lorsque toutes les valeurs de la série sont données l’une à la suite de l’autre.
- On calcule une moyenne pondérée lorsque chaque valeur de la série est associée à un effectif (ou coefficient).
Exemple
Comment calculer la moyenne simple de cette série statistique ?
1. Additionner les Valeurs
La 1ère étape est d’additionner toutes les valeurs de la série statistique. L’ordre dans lequel les nombres sont additionnés n’a aucune importance.
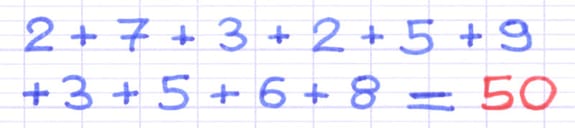
Toutes les valeurs de la série statistique sont additionnées.
2. Diviser par le Nombre de Valeurs
Le résultat obtenu à l’étape 1 est ensuite divisé par le nombre de valeurs au sein de la série statistique. Le nombre de valeurs correspond à la quantité de nombres additionnés précédemment. La valeur moyenne de la série est la réponse à cette division.
L’élève a reçu un total de 10 notes. Le résultat obtenu à l’étape 1 (50) est donc divisé par 10. La moyenne des notes de l’élève est de 5.
Exercice
Question 1
Quelle est, en moyenne, la taille du nez des profs de maths de ce collège ?
Question 2
Laquelle de ces propositions est vraie ?
Question 3
Jean-Bernard, un élève très studieux, a une moyenne de 19 en mathématiques (arrondie à l’unité près). L’une de ces quatre propositions représente son relevé de notes, laquelle ?