Calculer la Probabilité d’un Événement Contraire
Théorie
Deux événements sont contraires si l’un se réalise lorsque l’autre ne se réalise pas. La somme des probabilités de deux événements contraires est égale à 1. Deux événements contraires sont incompatibles, car ils ne possèdent aucune issue commune.
Exemple
Exercice : "Lorsqu’on lance une pièce de monnaie équilibrée (non truquée), la probabilité d’obtenir face est de 0,5. Calculer la probabilité d’obtenir pile".
Les événements "obtenir face" et "obtenir pile" sont deux événements contraires. Dans cette expérience aléatoire, soit on obtient face, soit on obtient pile.
L’événement F est le contraire de l’événement F. La barre horizontale indique qu’il s’agit d’un événement contraire.
Propriété : "La somme des probabilités de deux événements contraires est égale à 1".
La somme des probabilités des événements "obtenir face" et "obtenir pile" est donc égale à 1. On peut se servir de cette propriété pour créer une équation permettant de calculer la probabilité d’obtenir pile.
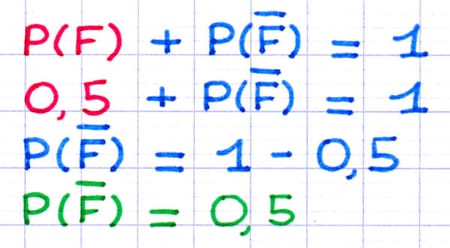
La probabilité d’obtenir pile est de 0,5.
Exemple
Exercice : "On pioche au hasard une boule dans une urne contenant des boules rouges, bleues et jaunes. La probabilité d’obtenir une boule bleue est de 0,4. Calculer la probabilité d’obtenir une boule jaune ou rouge".
"Obtenir une boule bleue" et "obtenir une boule jaune ou rouge" sont deux événements contraires. Dans cette expérience aléatoire, soit on obtient une boule bleue, soit on obtient une boule jaune ou rouge.
B et B sont deux événements contraires.
Propriété : "La somme des probabilités de deux événements contraires est égale à 1".
La somme des probabilités des événements "obtenir une boule bleue" et "obtenir une boule jaune ou rouge" est donc égale à 1. On peut se servir de cette propriété pour créer une équation permettant de calculer la probabilité d’obtenir une boule jaune ou rouge.
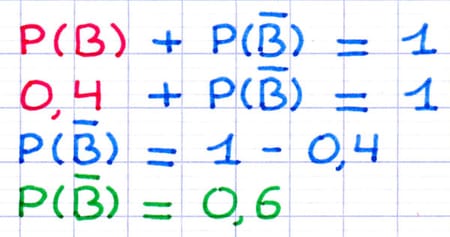
La probabilité d’obtenir une boule jaune ou rouge est de 0,6.
Exemple
Exercice : "Lorsqu’on lance un dé équilibré (non truqué), la probabilité d’obtenir un nombre inférieur ou égal à 2 est de 1/3. Calculer la probabilité d’obtenir un nombre supérieur ou égal à 3".
"Obtenir un nombre inférieur ou égal à 2" et "obtenir un nombre supérieur ou égal à 3" sont deux événements contraires. Dans cette expérience aléatoire, soit on obtient un nombre inférieur ou égal à 2, soit on obtient un nombre supérieur ou égal à 3.
D et D sont deux événements contraires.
Propriété : "La somme des probabilités de deux événements contraires est égale à 1".
La somme des probabilités des événements "obtenir un nombre inférieur ou égal à 2" et "obtenir un nombre supérieur ou égal à 3" est donc égale à 1. On peut se servir de cette propriété pour créer une équation permettant de calculer la probabilité d’obtenir un nombre supérieur ou égal à 3.
La probabilité d'obtenir un nombre supérieur ou égal à 3 est de 2/3.
Exercice
Question 1
On lance une pièce de monnaie truquée de telle façon que la probabilité d’obtenir face est de 0,75. Quelle est la probabilité d’obtenir pile ?
Question 2
Laquelle de ces propositions est vraie ?
Question 3
On pioche au hasard une boule au sein d’un chapeau contenant des boules bleues, rouges et vertes. Sachant que la probabilité d’obtenir une boule bleue est de 0,4, quelle est la probabilité d’obtenir une boule rouge ?