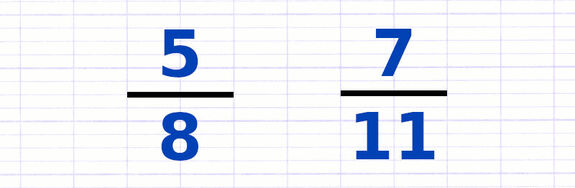
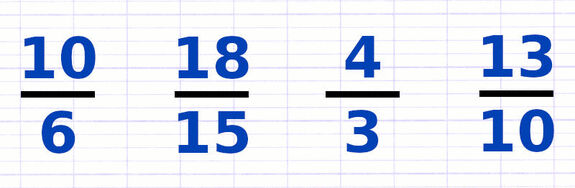
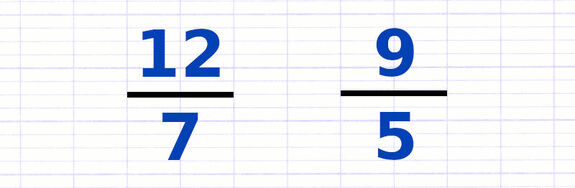Comparer des Fractions (Dénominateurs Différents)
Théorie
Comparer des fractions consiste à déterminer si une fraction est supérieure, inférieure ou égale à une autre fraction. La comparaison s’établit en utilisant les signes de comparaison. Pour effectuer la comparaison, on place les fractions sur un dénominateur commun.
Exemple
Comment comparer les fractions 9/4 et 8/3 ? Ces 2 fractions possèdent des dénominateurs différents (4 et 3).
1. Placer les Fractions sur un Dénominateur Commun
La 1re étape est de trouver un dénominateur commun en dressant, par ordre croissant, la liste des multiples de chaque dénominateur. Le dénominateur commun correspond au plus petit commun multiple (PPCM) des dénominateurs.
On trouve le dénominateur commun (12) grâce à la liste des multiples de chaque dénominateur.
Chaque fraction est ensuite transformée afin de faire apparaître le dénominateur commun. Cette transformation s’effectue en multipliant par un même nombre le numérateur et le dénominateur de chaque fraction.
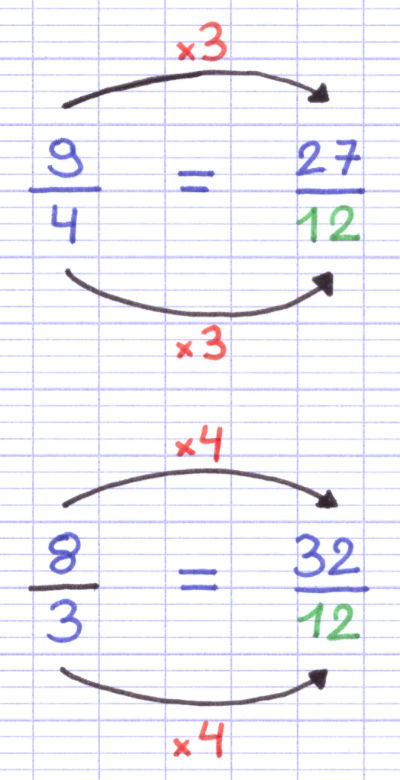
En multipliant par 3 le dénominateur de la 1re fraction, on obtient le dénominateur commun. On multiplie donc également le numérateur par 3. En multipliant par 4 le dénominateur de la 2e fraction, on obtient le dénominateur commun. On multiplie donc également le numérateur par 4.
2. Comparer les Numérateurs
Comparer des fractions partageant un dénominateur commun s’effectue en comparant les numérateurs :
- La plus grande fraction est celle dont le numérateur est le plus grand.
- La plus petite fraction est celle dont le numérateur est le plus petit.
- Les fractions sont égales si les numérateurs sont égaux.
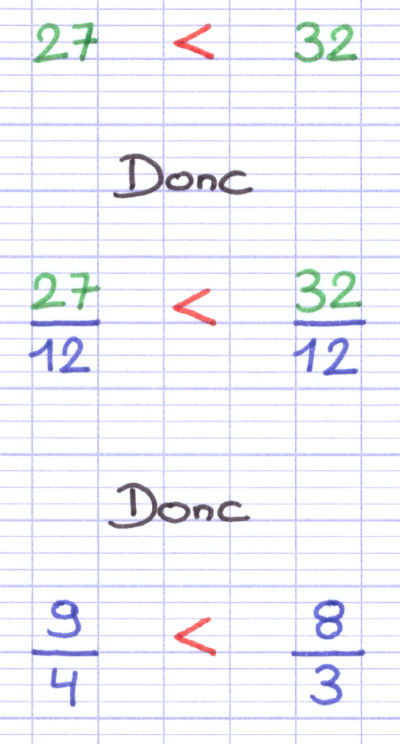
Le numérateur de la 1re fraction est supérieur au numérateur de la 2e fraction. La 1re fraction est donc supérieure à la 2e fraction.
Exercices
Question 1
Quelle technique permet de comparer le plus facilement ces deux fractions ?
Question 2
Laquelle de ces comparaisons est correcte ?
Question 3
Laquelle de ces fractions est la plus petite ?