Comparer des Nombres Relatifs
Théorie
Les nombres relatifs désignent l’ensemble des nombres positifs et négatifs. Comparer des nombres relatifs consiste à déterminer si un nombre est inférieur, supérieur ou égal à un autre. On utilise les signes de comparaison pour indiquer qu’un nombre est plus petit, plus grand ou égal à un autre.
3 signes de comparaison : strictement inférieur, égal et strictement supérieur. Ce sont les plus couramment utilisés, mais il en existe d’autres.
Exemples
Comparer 2 Nombres Positifs
Comment comparer ces 2 nombres relatifs positifs ?
La comparaison de 2 nombres entiers positifs s’effectue en analysant leurs différents chiffres. Si les 2 nombres ont la même quantité de chiffres, on compare chaque chiffre 1 à 1 en commençant par la gauche. Dès qu’un chiffre est plus grand qu’un autre, on peut conclure que le nombre auquel il appartient est strictement supérieur.
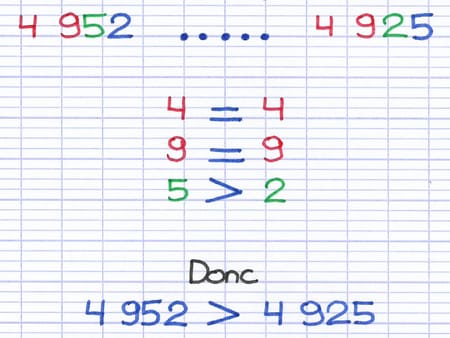
Le 1er chiffre des 2 nombres relatifs est identique (4).
Le 2e chiffre des 2 nombres relatifs est identique (9).
Le 3e chiffre de 4952 (5) est plus grand que celui de 4925 (2).
4952 est donc strictement supérieur à 4925.
Si tous les chiffres sont identiques, alors les 2 nombres relatifs sont égaux. Si les 2 nombres entiers positifs n’ont pas la même quantité de chiffres, le plus grand est celui avec le plus de chiffres.
Comparer 2 Nombres Négatifs
Comment comparer ces 2 nombres relatifs négatifs ?
Pour comparer 2 nombres entiers négatifs, on commence par retirer le signe "-" devant chaque nombre relatif. On obtient ainsi 2 nombres positifs.
Les nombres négatifs se transforment en nombres positifs.
On utilise ensuite la technique de comparaison précédente relative aux nombres positifs. On compare chaque chiffre 1 à 1 et on s’arrête dès que l’un est inférieur ou supérieur à l’autre.
Le 1er chiffre des 2 nombres relatifs est identique (2).
Le 2e chiffre de 274 (7) est plus petit que celui de 289 (8).
274 est donc strictement inférieur à 289.
On ajoute ensuite le signe "-" devant chaque nombre relatif et on inverse le signe de comparaison :
- Si le signe était inférieur, il devient supérieur.
- Si le signe était supérieur, il devient inférieur.
Le signe de comparaison s’inverse quand les 2 nombres relatifs redeviennent négatifs.
-274 est strictement supérieur à -289.
Cette technique repose sur la propriété ci-dessous, dans laquelle A et B représentent 2 nombres différents.
Propriété : Si A est plus grand que B, alors -A est plus petit que -B.
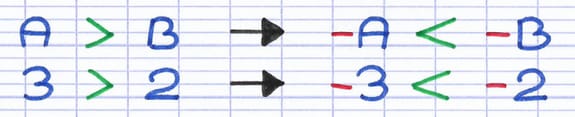
La technique de comparaison des nombres négatifs repose sur cette propriété mathématique.
Comparer 2 Nombres de Signes Différents
Comment comparer ces 2 nombres relatifs de différents signes ?
La comparaison de 2 nombres relatifs possédant des signes différents s’effectue très rapidement :
- Le nombre positif est toujours strictement supérieur au nombre négatif.
- Le nombre négatif est toujours strictement inférieur au nombre positif.
Le nombre positif 72 est strictement supérieur au nombre négatif -647.
Droite graduée
Une droite graduée est un bon outil pour comparer des nombres relatifs. Le plus grand nombre relatif est toujours celui qui se trouve le plus à droite sur la droite graduée.
Placer des nombres relatifs sur une droite graduée permet de facilement les comparer. "-1" est à droite de "-4", donc "-1" est strictement supérieur à "-4".
La comparaison des nombres relatifs peut également s’effectuer en analysant leur distance par rapport à zéro :
- Si les 2 nombres sont positifs, le plus grand est toujours le plus éloigné de zéro.
- Si les 2 nombres sont négatifs, le plus grand est toujours le plus proche de zéro.
Exercices
Question 1
Laquelle de ces comparaisons est correcte ?
Question 2
Si A est strictement supérieur à B, que peut-on affirmer ?
Question 3
Laquelle de ces propositions est fausse ?