Comprendre les Propriétés d'Agrandissement et Réduction
En géométrie, l'agrandissement et la réduction d'une figure ont des effets sur les longueurs, les aires et les volumes.
Dans cette fiche, nous te présentons toutes les propriétés de ces transformations.
-
1
Les longueurs
Agrandir ou réduire une figure s'effectue en multipliant la longueur de tous ses côtés par un même nombre (k):
- Il s'agit d'un agrandissement lorsque k > 1.
- Il s'agit d'une réduction lorsque 0 < k < 1.
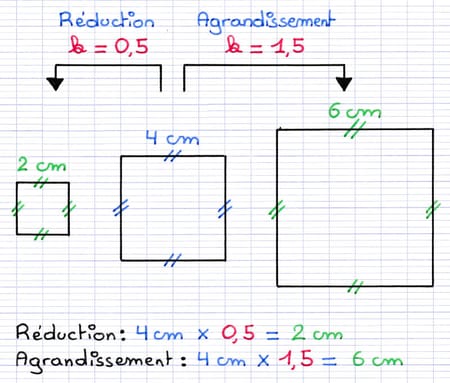
Lors d'un agrandissement ou réduction, toutes les longueurs sont multipliées par un même nombre. Le nombre k est un coefficient de proportionnalité:
- Il s'agit d'un coefficient d'agrandissement (ou facteur d'agrandissement) lorsque k > 1.
- Il s'agit d'un coefficient de réduction (ou facteur de réduction) lorsque 0 < k < 1.
Les longueurs des côtés de la figure de départ et de la figure transformée sont donc proportionnelles.
-
2
Les aires
L'aire d'une figure transformée par agrandissement ou réduction varie selon le coefficient de proportionnalité (k).
Lorsque les longueurs d'une figure sont multipliées par k, son aire est multipliée par k2.
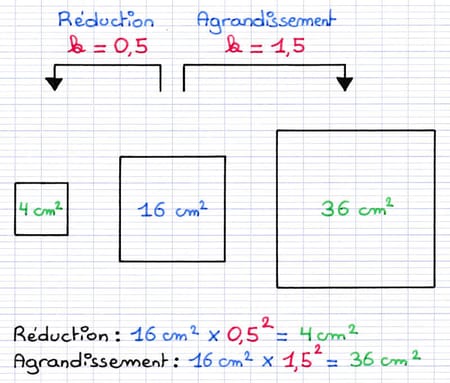
Lors d'un agrandissement ou réduction de rapport k, les aires sont multipliées par k2. -
3
Les volumes
Le volume d'un solide (figure géométrique en 3D) transformé par agrandissement ou réduction varie selon le coefficient de proportionnalité (k).
Lorsque les longueurs d'un solide sont multipliées par k, son volume est multiplié par k3.
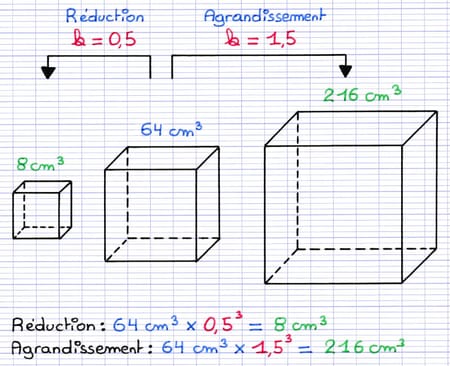
Lors d'un agrandissement ou réduction de rapport k, les volumes sont multipliés par k3. -
4
Les angles
Lors d'un agrandissement ou d'une réduction, la mesure de chaque angle est conservée.
Les mesures des angles de la figure de départ et de la figure transformée sont donc identiques.
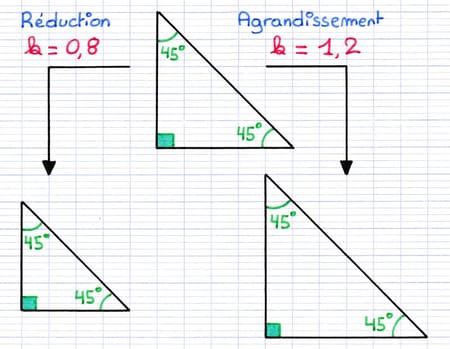
Lors d'un agrandissement ou réduction, la mesure des angles est conservée.
Vérifiez si votre puissance mathématique a augmenté !
Associez chaque coefficient d'agrandissement / réduction à son effet, puis comparez votre réponse avec la correction.
