Comprendre les Propriétés de la Symétrie Axiale
Théorie
2 figures sont symétriques par rapport à une droite si elles sont superposables par pliage le long de cette droite. L’axe de symétrie est le nom donné à cette droite.
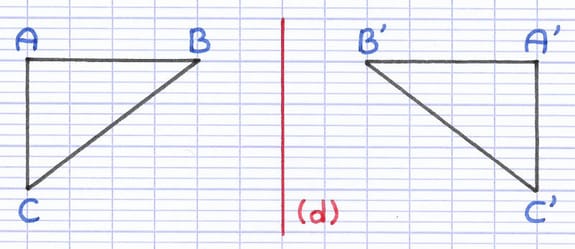
Ces 2 triangles sont symétriques par rapport à la droite (d). Si on effectue un pliage le long de la droite (d), les 2 triangles se superposent l’un sur l’autre. L’axe de symétrie est la droite (d).
Propriétés de conservation
La symétrie axiale possède des propriétés de conservation. L’image d’une figure par symétrie axiale conserve les longueurs, les alignements, les angles et l’aire de la figure de départ. Des figures symétriques ont donc des longueurs, des alignements, des angles et des aires identiques.
Longueurs
Propriété : "Les segments de 2 figures symétriques ont des longueurs identiques."
Dans une symétrie axiale, la longueur des segments est donc conservée. En conséquence, 2 figures symétriques ont également un périmètre identique.
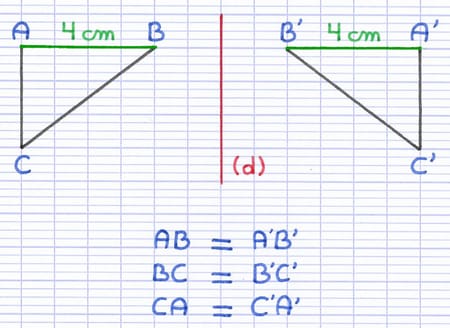
La symétrie axiale conserve la longueur des segments.
La longueur du segment [AB] est de 4 cm.
La longueur du segment [A’B'] est également de 4 cm.
Alignements
Propriété : "Les points de 2 figures symétriques sont alignés de la même façon."
Dans une symétrie axiale, l’alignement des points est donc conservé. En conséquence, le parallélisme est conservé. Les symétriques de 2 droites parallèles sont également parallèles.
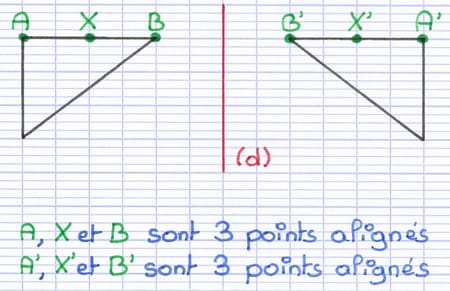
La symétrie axiale conserve l’alignement des points.
Les points A, X et B sont alignés.
Les points A’, X’ et B’ sont également alignés.
Angles
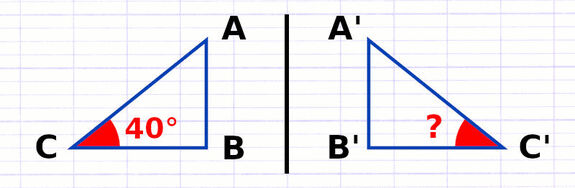
Propriété : "Les angles de 2 figures symétriques ont des mesures identiques."
Dans une symétrie axiale, la mesure des angles est donc conservée.
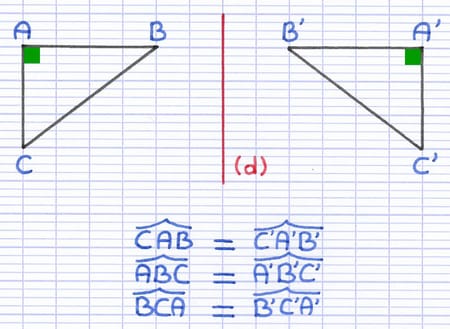
La symétrie axiale conserve la mesure des angles.
L’angle CAB mesure 90°.
L’angle C’A’B’ mesure également 90°.
Aires
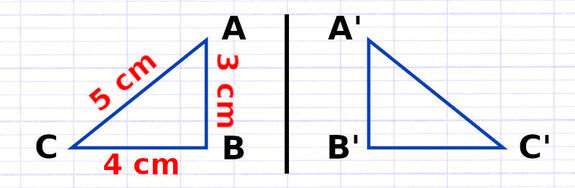
Propriété : "L’aire de 2 figures symétriques est identique."
Dans une symétrie axiale, l’aire des figures est donc conservée.
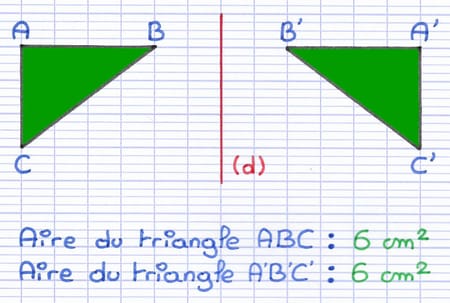
La symétrie axiale conserve l’aire des figures.
L’aire du triangle ABC est de 6 cm².
L’aire du triangle A’B’C’ est également de 6 cm².
Exercices
Question 1
Le triangle A’B’C’ est l’image du triangle ABC par symétrie axiale. Quelle est la mesure de l’angle A’C’B’ ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
Le triangle A’B’C’ est l’image du triangle ABC par symétrie axiale. Quelle est la longueur de [A’C’] ?