Construire l’Image d’un Segment par Symétrie Centrale
Théorie
Les constructions d’une symétrie centrale s’effectuent autour d’un point appelé centre de symétrie. L’image d’un segment par symétrie centrale est le symétrique du segment de l’autre côté du centre de symétrie.
Exemple
![Segment [AB] dont on cherche à construire l’image par symétrie centrale de centre O.](/img/fiche/136/comment-construire-image-segment-symetrie-centrale.jpg "Construire l’image d’un segment par symétrie centrale")
Comment construire l’image du segment [AB] par la symétrie centrale de centre O ? Le centre de symétrie est le point O.
Tracer 2 Demi-Droites
La 1re étape est de tracer, à partir de chaque extrémité du segment, une demi-droite qui passe par le centre de symétrie. La longueur de chaque demi-droite doit être au moins le double de la distance entre l’extrémité et le centre.
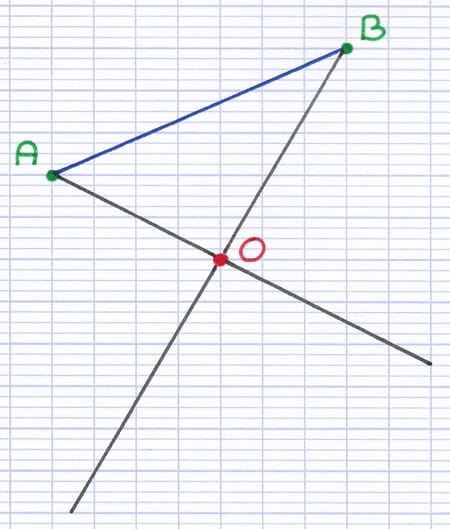
La construction de l’image du segment [AB] commence par tracer 2 demi-droites [AO) et [BO). Chaque demi-droite démarre d’une extrémité (A ou B) et passe par le centre de symétrie O.
Trouver les Images des Extrémités
À l’aide d’une règle, on mesure ensuite la distance entre chaque extrémité du segment et le centre de symétrie. Pour trouver les images des 2 extrémités, on reporte chaque distance de l’autre côté du centre de symétrie, sur la demi-droite.
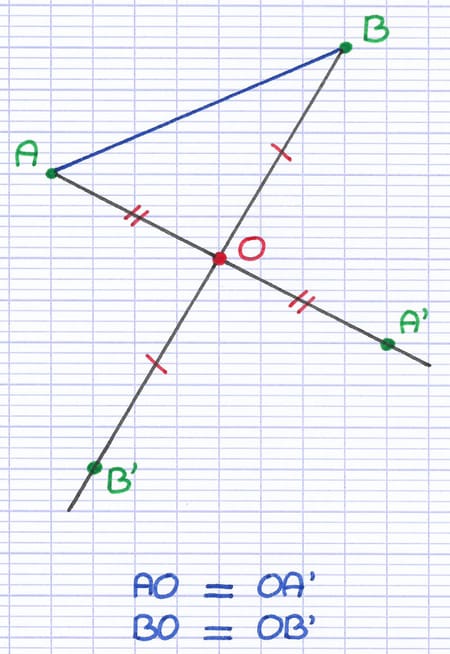
Chaque extrémité du segment est un point dont on peut trouver l’image par symétrie centrale. A’ et B’ sont les images (les symétriques) des points A et B par la symétrie centrale de centre O.
Il est également possible de trouver l’image des extrémités avec un compas. La technique est expliquée en détails au sein de la fiche de synthèse ci-dessous.
Tracer l’Image du Segment
La dernière étape est de tracer le segment qui relie l’image des 2 extrémités. Le segment ainsi obtenu est l’image (le symétrique) du segment de départ par symétrie centrale.
![Le segment [A’B’] est l’image du segment [AB] par symétrie centrale de centre O.](/img/fiche/136/image-segment-symetrie-centrale.jpg "Image d’un segment par symétrie centrale")
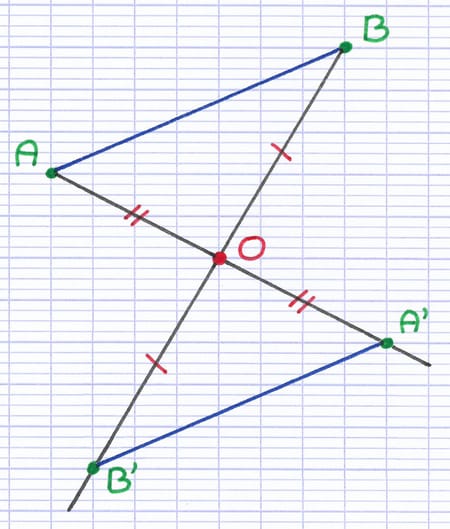
Le segment [A’B’] est l’image du segment [AB] par symétrie centrale de centre O.
Propriété
Propriété : "L’image d’un segment par symétrie centrale est un segment parallèle de même longueur".
![Les segments [AB] et [A’B’] symétriques par rapport au centre de symétrie O sont parallèles et de même longueur.](/img/fiche/136/segments-symetriques-centre-symetrie-parallele-longueur.jpg "Deux segments symétriques autour d’un centre de symétrie parallèles et de mêmes longueurs")
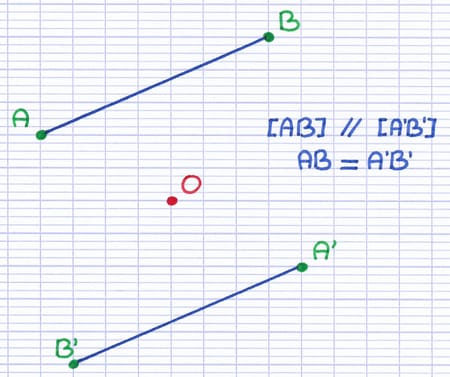
2 segments symétriques par rapport à un centre de symétrie sont parallèles et de longueurs identiques.
Cas particulier
Parfois, le centre de symétrie est situé sur le segment dont on souhaite construire l’image.
![Cas particulier d’un centre de symétrie O placé sur le segment [XY] dont on cherche à trouver le symétrique.](/img/fiche/136/centre-symetrie-appartient-segment.jpg "Centre de symétrie appartenant au segment")
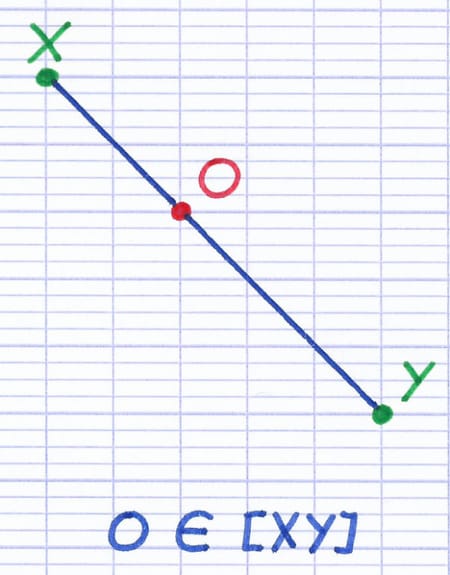
Le centre de symétrie O appartient au segment [XY].
Dans ces circonstances, l’image du segment par symétrie centrale se superpose sur le segment de départ.
![L’image du segment [XY] par symétrie centrale de centre O est le segment [X’Y’] superposé sur la même droite, car le centre de symétrie appartient aux deux droites.](/img/fiche/136/image-segment-centre-symetrie.jpg "Image d’un segment passant par le centre de symétrie")
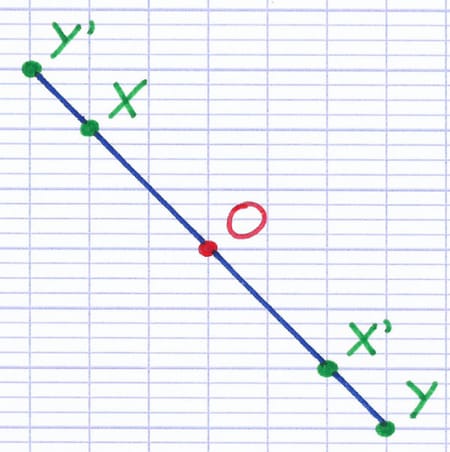
Les deux segments symétriques [XY] et [X’Y’] sont l’un sur l’autre.
Quiz
Question 1
Quelle est l’image du segment [AB] par la symétrie centrale de centre O ?
Question 2
Laquelle de ces propriétés est vraie ?
Question 3
Quelle est l’image du segment [BD] par la symétrie centrale de centre O ?