Décomposer un Nombre Entier par Rang
Théorie
En sixième, la décomposition d’un nombre entier s’effectue selon un rang précis ou selon chaque rang. Dans les 2 cas, il est conseillé de placer le nombre entier dans un tableau de numération pour faciliter sa décomposition.
Le tableau de numération facilite la décomposition par rang des nombres entiers.
Exemple
La décomposition d’un nombre entier selon un rang précis commence par une multiplication et se termine par une addition.
Comment décomposer 32 469 selon le rang des centaines ?
1. Trouver le Nombre du Rang
La 1re étape est de trouver le nombre du rang de la décomposition en plaçant le nombre entier au sein d’un tableau de numération. Le nombre du rang de la décomposition est l’ensemble des chiffres à l’intérieur et à gauche de la colonne correspondante.
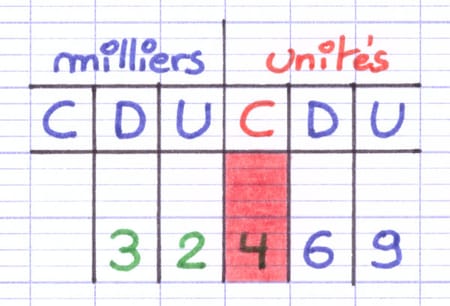
On souhaite décomposer 32 469 selon le rang des centaines. Le rang de la décomposition est donc le rang des centaines. Le nombre de centaines est l’ensemble des chiffres à l’intérieur et à gauche de la colonne des centaines. Dans 32 469, le nombre de centaines est 324.
2. Déterminer le Coefficient du Rang
On cherche ensuite le coefficient correspondant au rang de la décomposition. Chaque rang est associé à un coefficient :
- Le rang des unités a pour coefficient 1.
- Le rang des dizaines a pour coefficient 10.
- Le rang des centaines a pour coefficient 100.
- ...
À chaque déplacement d’une colonne vers la gauche dans le tableau de numération, le coefficient est 10x plus grand.
Le rang de la décomposition est celui des centaines. Le coefficient des centaines est 100.
3. Multiplier le Nombre du Rang par son Coefficient
L’étape suivante est d’écrire la multiplication entre le nombre du rang (étape 1) et le coefficient du rang (étape 2). Cette multiplication est la 1re partie de la décomposition. La multiplication est généralement notée entre parenthèses afin de rendre la décomposition plus claire.
Le nombre de centaines est 324 (étape 1). Le coefficient des centaines est 100 (étape 2). La décomposition démarre donc par (324 x 100).
4. Ajouter le Nombre Restant
Il ne reste plus qu’à ajouter le nombre restant à la fin de la décomposition sous la forme d’une addition. Le nombre restant est l’ensemble des chiffres à droite de la colonne du rang de la décomposition.
Le nombre restant est l’ensemble des chiffres à droite de la colonne des centaines (69). Le nombre restant est ajouté (+) à la fin de la décomposition. Le résultat de la décomposition est donc (324 x 100) + 69.
Exemple
Décomposer un nombre entier selon chaque rang s’effectue en créant une multiplication pour chaque rang.
Comment décomposer 32 469 selon chaque rang ?
1. Trouver le Chiffre de Chaque Rang
La 1re étape est de trouver le chiffre de chaque rang en plaçant le nombre entier au sein d’un tableau de numération. Le chiffre d’un rang est l’unique chiffre positionné dans la colonne correspondante.
Le nombre entier 32 469 possède 5 chiffres appartenant chacun à un rang.
Le chiffre des dizaines de milliers est 3.
Le chiffre des milliers est 2.
Le chiffre des centaines est 4.
Le chiffre des dizaines est 6.
Le chiffre des unités est 9.
2. Multiplier chaque Chiffre par son Coefficient
L’étape suivante est d’écrire la multiplication entre chaque chiffre et le coefficient associé à son rang. Chaque rang est associé à un coefficient :
- Le rang des unités a pour coefficient 1.
- Le rang des dizaines a pour coefficient 10.
- Le rang des centaines a pour coefficient 100.
- ...
À chaque déplacement d’une colonne vers la gauche dans le tableau de numération, le coefficient est 10x plus grand.
Le chiffre des dizaines de milliers (3) est multiplié par 10 000.
Le chiffre des milliers (2) est multiplié par 1 000.
Le chiffre des centaines (4) est multiplié par 100.
Le chiffre des dizaines (6) est multiplié par 10.
Le chiffre des unités (9) est multiplié par 1.
3. Additionner toutes les Multiplications
Il ne reste plus qu’à additionner toutes les multiplications de l’étape 2 afin d’obtenir la décomposition du nombre entier. Les multiplications sont :
- Classées par ordre décroissant (du rang le plus grand au rang le plus petit).
- Chacune notées entre parenthèses afin de rendre la décomposition plus claire.
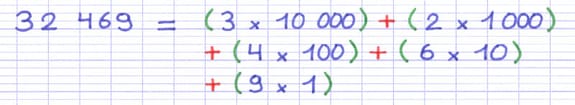
Les multiplications de l’étape 2 sont additionnées par ordre décroissant.
La multiplication du rang des unités n’est généralement pas notée, car il est inutile de multiplier un nombre par 1. La multiplication du rang des unités est remplacée par le chiffre des unités, sans multiplication ni parenthèse.
La multiplication du rang des unités (9 x 1) est remplacée par le chiffre des unités (9). Le résultat de la décomposition est donc (3 x 10 000) + (2 x 1 000) + (4 x 100) + (6 x 10) + 9.
Exercices
Question 1
Quelle est la décomposition de ce nombre entier selon le rang des dizaines ?
Question 2
Quelle est la décomposition de ce nombre entier selon chaque rang ?
Question 3
Quelle est la décomposition de ce nombre entier selon le rang des centaines de milliers ?