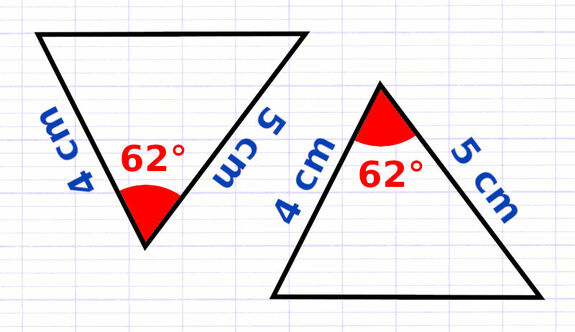
Découvrir les 3 Cas d’Égalité des Triangles
Théorie
Deux triangles sont égaux s’ils ont exactement les mêmes dimensions :
- Leurs côtés sont de même longueur.
- Leurs angles sont de même mesure.
Des triangles égaux sont superposables (si on les découpe, ils se recouvrent parfaitement). Les côtés, angles et sommets identiques qui se superposent sont appelés des côtés, angles et sommets homologues.
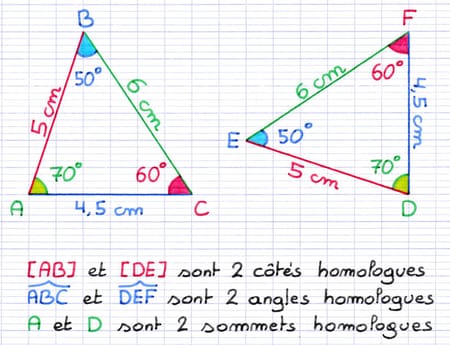
Les triangles ABC et DEF sont égaux.
ils ont 3 paires d’angles homologues : ABC et DEF, BCA et EFD, CAB et FDE.
ils ont 3 paires de côtés homologues : [AB] et [DE], [BC] et [EF], [CA] et [FD].
ils ont 3 paires de sommets homologues : A et D, B et E, C et F.
Cas d’égalité
Pour démontrer que 2 triangles sont égaux, il n’est pas nécessaire de vérifier que tous leurs côtés et leurs angles ont la même mesure. La démonstration peut s’effectuer plus rapidement en utilisant l’un des 3 cas d’égalité des triangles ci-dessous.
3 Côtés (CCC)
Cas d’égalité CCC : "Si 2 triangles ont leurs côtés deux à deux de même longueur, alors ces 2 triangles sont égaux".
On peut donc démontrer que 2 triangles sont égaux en indiquant qu’ils ont 3 paires de côtés de même longueur.
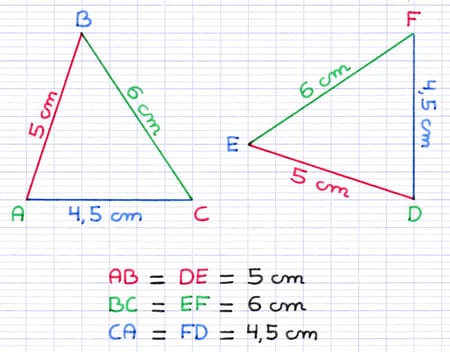
Les triangles ABC et DEF sont égaux, car ils ont leurs côtés 2 à 2 de même longueur.
La démonstration à l’aide du cas d’égalité CCC possède un avantage et un inconvénient :
- Avantage : Il n’est pas nécessaire de comparer la mesure des angles.
- Inconvénient : Il faut connaître la longueur de tous les côtés.
1 Angle entre 2 Côtés (CAC)
Cas d’égalité CAC : "Si 2 triangles ont un angle de même mesure compris entre des côtés deux à deux de même longueur, alors ces 2 triangles sont égaux".
On peut donc démontrer que 2 triangles sont égaux en indiquant qu’ils ont 1 paire d’angles de même mesure entre 2 paires de côtés de même longueur.
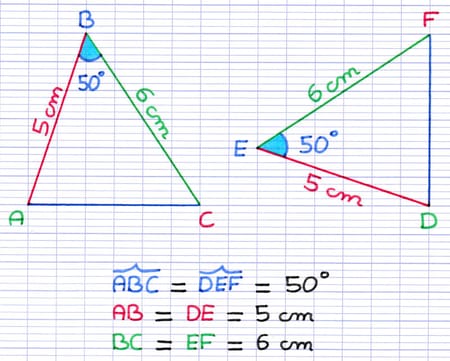
Les triangles ABC et DEF sont égaux, car ils ont un angle de même mesure compris entre des côtés 2 à 2 de même longueur.
La démonstration à l’aide du cas d’égalité CAC possède un avantage et un inconvénient :
- Avantage : 1 paire d’angles de même mesure suffit.
- Inconvénient : La paire d’angles de même mesure doit être entre 2 paires de côtés de même longueur.
1 Côté entre 2 Angles (ACA)
Cas d’égalité ACA : "Si 2 triangles ont un côté de même longueur et des angles adjacents à ce côté deux à deux de même mesure, alors ces 2 triangles sont égaux".
On peut donc démontrer que 2 triangles sont égaux en indiquant qu’ils ont 1 paire de côtés de même longueur entre 2 paires d’angles de même mesure.
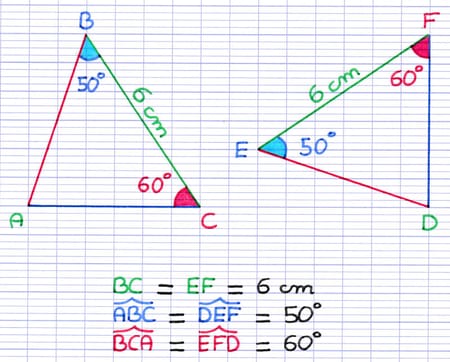
Les triangles ABC et DEF sont égaux, car ils ont un côté de même longueur et des angles adjacents à ce côté 2 à 2 de même mesure.
La démonstration à l’aide du cas d’égalité ACA possède un avantage et un inconvénient :
- Avantage : 1 paire de côtés de même longueur suffit.
- Inconvénient : La paire de côtés de même longueur doit être entre 2 paires d’angles de même mesure.
Exercice
Question 1
Quel cas d’égalité des triangles permet de démontrer que ces deux triangles sont égaux ?
Question 2
Quelle proposition correspond à la définition de deux triangles égaux ?
Question 3
Laquelle de ces propositions n’est pas un cas d’égalité des triangles ?