Effectuer la Division Décimale de 2 Nombres Entiers
Théorie
La division décimale est une technique de calcul qui permet de diviser 2 nombres entiers pour obtenir un quotient décimal :
- Le dividende est le nombre qui est divisé.
- Le diviseur est le nombre qui divise.
- Le quotient est le résultat de la division.
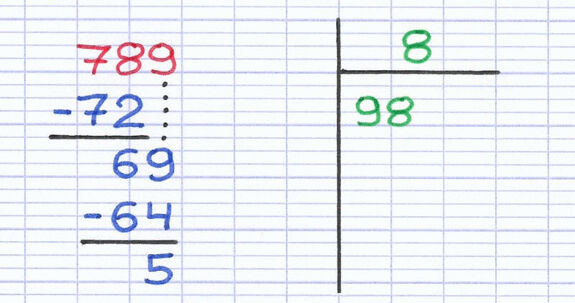
Il est important de maîtriser la division euclidienne avant de s’aventurer à effectuer une division décimale.
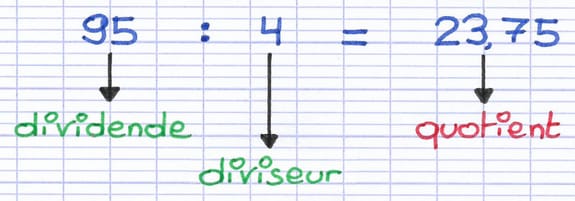
Le dividende est 95.
Le diviseur est 4.
Le quotient décimal est 23,75.
Exemple
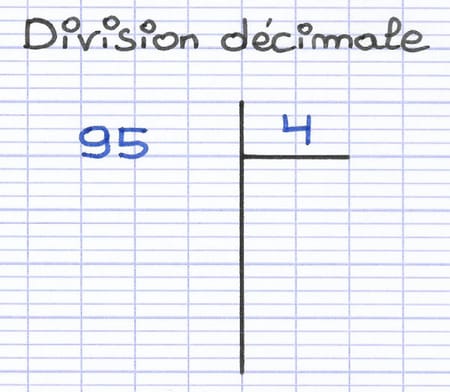
Comment effectuer la division décimale de 95 par 4 ?
Effectuer une Division Euclidienne
La 1re étape est d’effectuer une division euclidienne. La division euclidienne consiste à diviser le dividende par le diviseur afin d’obtenir un quotient et un reste.
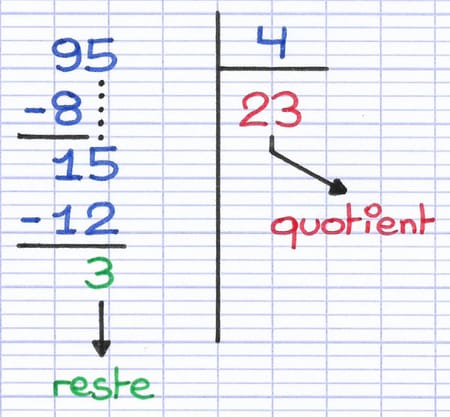
Le quotient de la division euclidienne est 23.
Le reste de la division euclidienne est 3.
Contrairement à la division euclidienne, la division décimale se poursuit jusqu’à ce que le reste soit "0".
Trouver le 1er Chiffre Décimal
Lorsque la division euclidienne est terminée, on ajoute un "0" derrière le reste et on place une virgule derrière le quotient. On se pose alors cette question : "Par combien faut-il multiplier le diviseur pour obtenir le plus grand nombre inférieur ou égal au reste ?".
La réponse à cette question le 1er chiffre décimal du quotient.
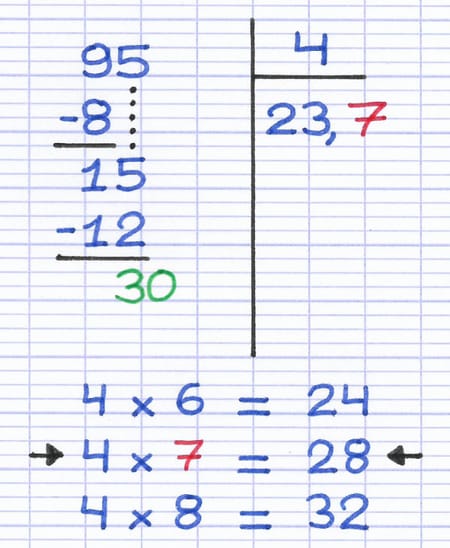
Le plus grand nombre inférieur ou égal à 30 est obtenu en multipliant le diviseur par 7. Le 1er chiffre décimal du quotient est donc 7.
Calculer le Nouveau Reste
La suite des opérations s’effectue comme une division euclidienne. On multiplie le diviseur par le chiffre derrière la virgule, puis on effectue une soustraction pour obtenir un nouveau reste.

Le nouveau reste de la division décimale est 2.
Recommencer jusqu’à Obtenir un Reste Nul
La division décimale se termine uniquement lorsqu’on obtient un reste égal à "0". Tant que le reste est différent de "0", on recommence donc les 2 étapes précédentes.

La division décimale est terminée, car le reste est nul (0). Le quotient exact est 23,75.
Valeur approchée
Certaines divisions décimales ne s’arrêtent jamais (le reste n’est jamais nul). Cette situation apparaît lorsque le quotient possède une partie décimale infinie.

La division décimale de 10 par 3 ne s’arrête jamais, car le reste n’est jamais nul (0). La partie décimale du quotient est infinie.
Dans ces circonstances, il est impossible de calculer le quotient exact de la division décimale. Par contre, on peut donner une valeur approchée du quotient :
- La valeur approchée au dixième près possède 1 chiffre décimal.
- La valeur approchée au centième près possède 2 chiffres décimaux.
- La valeur approchée au millième près possède 3 chiffres décimaux.
- ...

3,3 est la valeur approchée au dixième près du quotient.
3,33 est la valeur approchée au centième près du quotient.
3,333 est la valeur approchée au millième près du quotient.
Cas particulier
Lorsque le dividende est plus petit que le diviseur, la division décimale est un peu particulière. La 1re étape est de trouver le quotient et le reste de la division euclidienne. Ce quotient est toujours « 0 », car le diviseur est plus grand que le dividende.
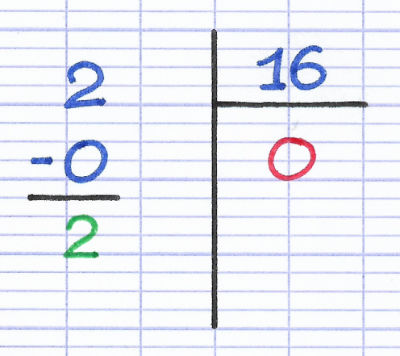
Le dividende (2) est plus petit que le diviseur (16).
Le quotient de la division euclidienne est 0.
Le reste de la division euclidienne est 2.
Les étapes suivantes sont les mêmes que pour une division décimale classique. On ajoute un "0" derrière le reste, on place une virgule derrière le quotient, et on poursuit les calculs normalement. La division décimale se termine lorsqu’on obtient un reste nul.

Le reste de la division décimale est nul (0). Le quotient exact de la division décimale est 0,125.
Lorsque le dividende est plus petit que le diviseur, la partie entière du quotient est toujours "0".
Équation
Il existe une équation mathématique qui unit les 3 éléments de la division décimale. Le dividende est toujours égal au produit (multiplication) du diviseur par le quotient exact (le reste est égal à 0).

Cette équation unit le dividende, le diviseur et le quotient exact d’une division décimale.
On peut utiliser cette équation pour vérifier que le quotient exact est correct :
- Si l’égalité est vraie, la division décimale est correcte.
- Si l’égalité est fausse, la division décimale contient une erreur.

Le dividende (95) est égal au produit du diviseur (4) par le quotient exact (23,75). L’égalité est vraie, la division décimale est donc correcte.