Effectuer une Division Euclidienne avec Reste
Théorie
La division euclidienne (également appelée division entière) s’effectue entre 2 nombres entiers :
- Le dividende est le nombre qui est divisé.
- Le diviseur est le nombre qui divise.
Effectuer une division euclidienne consiste à trouver le quotient et le reste de la division :
- Le quotient est le résultat principal de la division.
- Le reste est toujours inférieur au diviseur.
Exemple

Comment effectuer la division euclidienne de 812 par 3 ?
Le dividende est "812" et le diviseur est "3".
1. Poser la Division
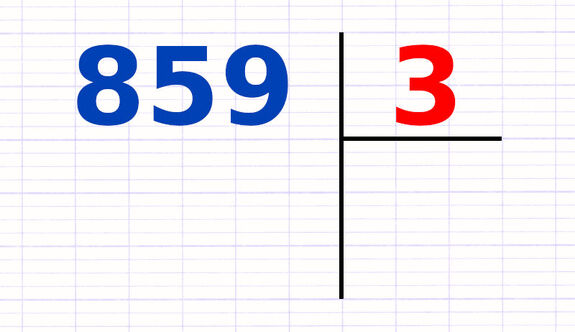
La 1re étape est de poser la division euclidienne sur sa feuille de papier. La division euclidienne s’effectue à partir de 2 droites perpendiculaires :
- Le dividende se note en haut à gauche de la droite verticale.
- Le diviseur se note en haut à droite de la droite verticale.
À la fin des calculs, le quotient apparaîtra en bas de la droite horizontale et le reste en bas à gauche de la droite verticale.
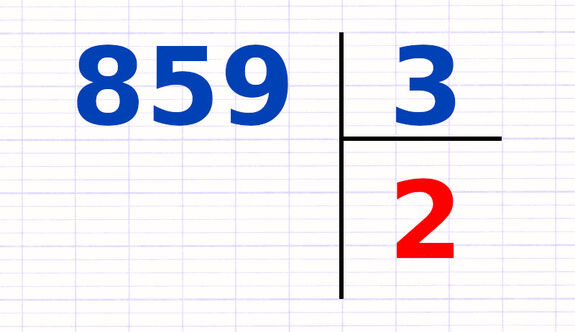
Deux droites séparent les éléments principaux de la division euclidienne : dividende, diviseur, quotient et reste.
2. Trouver le 1er Chiffre du Quotient
On repère ensuite le diviseur (en rouge) et le 1er chiffre en partant de la gauche du dividende (en vert). On se pose alors cette question : "Par combien faut-il multiplier le diviseur pour obtenir le plus grand nombre inférieur ou égal au 1er chiffre du dividende ?"
La réponse se note en-dessous de la droite horizontale. Il s’agit du 1er chiffre du quotient.

Le plus grand nombre inférieur ou égal à 8 est obtenu en multipliant le diviseur par 2. Le 1er chiffre du quotient de la division euclidienne est donc 2.
3. Multiplier par le Diviseur
L’étape suivante est de multiplier le 1er chiffre du quotient (en vert) par le diviseur (en rouge). La réponse se note en-dessous du 1er chiffre du dividende.

Le diviseur (3) est multiplié par le 1er chiffre du quotient (2).
4. Trouver le Reste Provisoire
On soustrait ensuite au 1er chiffre du dividende (en rouge) le résultat de la multiplication (en vert). La réponse se note en-dessous de la soustraction, il s’agit du reste provisoire de la division euclidienne. Ce reste est toujours inférieur au diviseur (si ce n’est pas le cas, une erreur a été commise aux étapes précédentes).
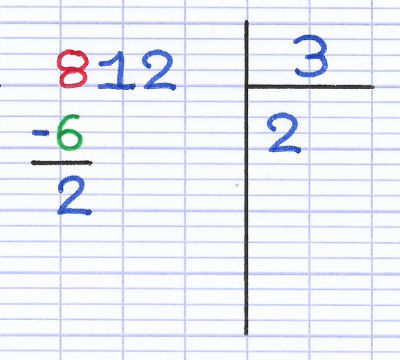
Soustraction du 1er chiffre du dividende (8) par le résultat de la multiplication (6). La réponse (2) est le reste provisoire de la division euclidienne. Le reste est inférieur au diviseur (2 < 3).
5. Descendre le Prochain Chiffre
L’étape suivante est de descendre le 2e chiffre du dividende (en rouge) à côté du reste provisoire (en vert). Ces 2 chiffres forment ensemble un nouveau reste.

Le 2e chiffre du dividende (1) descend à côté du reste provisoire (2) pour former un nouveau reste (21).
Il faut maintenant recommencer toutes les étapes précédentes ! Le quotient et le reste final apparaîtront lorsqu’il n’y aura plus aucun chiffre du dividende à descendre.
6. Répéter les Étapes Précédentes
Toutes les étapes précédentes sont maintenant répétées à partir de cette question : "Par combien faut-il multiplier le diviseur (en rouge) pour obtenir le plus grand nombre inférieur ou égal au reste (en vert) ?"
La réponse se note en-dessous de la droite horizontale. Il s’agit du 2e chiffre du quotient.
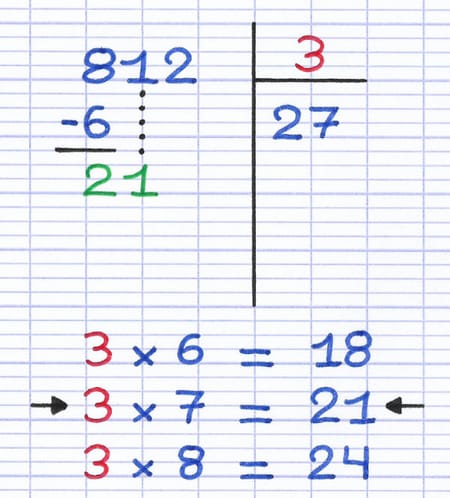
Le plus grand nombre inférieur ou égal à 21 est obtenu en multipliant le diviseur par 7. Le 2e chiffre du quotient de la division euclidienne est donc 7.
On multiplie ensuite le 2e chiffre du quotient (en vert) par le diviseur (en rouge). La réponse se note en-dessous du reste provisoire.
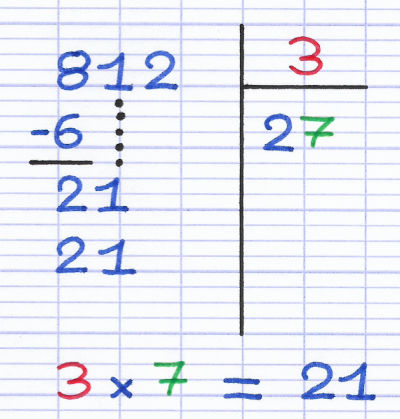
Le diviseur (3) est multiplié par le 2e chiffre du quotient (7).
On soustrait ensuite au reste provisoire (en rouge) le résultat de la multiplication (en vert). La réponse se note en-dessous de la soustraction, il s’agit du nouveau reste provisoire de la division euclidienne. Ce reste est toujours inférieur au diviseur (si ce n’est pas le cas, une erreur a été commise aux étapes précédentes).
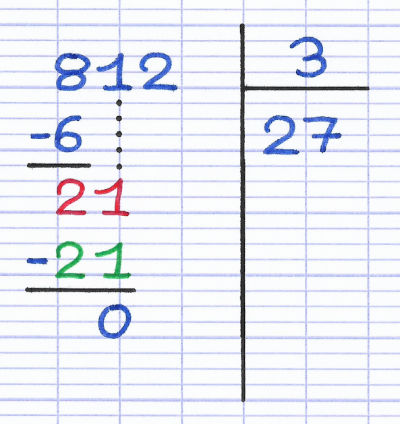
Soustraction du reste provisoire (21) par le résultat de la multiplication (21). La réponse (0) est le nouveau reste provisoire de la division euclidienne. Le reste est inférieur au diviseur (0 < 3).
La division euclidienne n’est pas terminée, car on peut encore descendre le dernier chiffre du dividende. On descend donc le 3e chiffre du dividende (en rouge) à côté du reste provisoire (en vert). Ces 2 chiffres forment ensemble un nouveau reste.
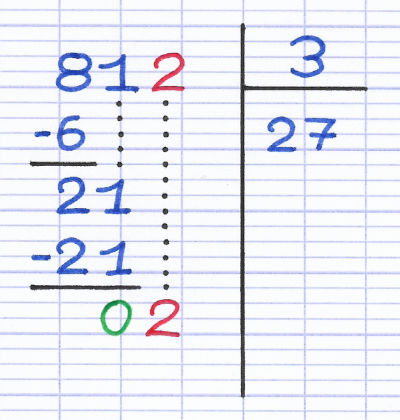
Le 3e chiffre du dividende (2) descend à côté du reste provisoire (0) pour former un nouveau reste (02).
À partir d’ici, on répète une nouvelle fois toutes les étapes précédentes en commençant par cette question : "Par combien faut-il multiplier le diviseur (en rouge) pour obtenir le plus grand nombre inférieur ou égal au reste (en vert) ?"
La réponse se note en-dessous de la droite horizontale, c’est le 3e chiffre du quotient.

Le plus grand nombre inférieur ou égal à 2 est obtenu en multipliant le diviseur par 0. Le 3e chiffre du quotient de la division euclidienne est donc 0.
Le 3e chiffre du quotient (en vert) est ensuite multiplié par le diviseur (en rouge). La réponse se note en-dessous du reste provisoire.
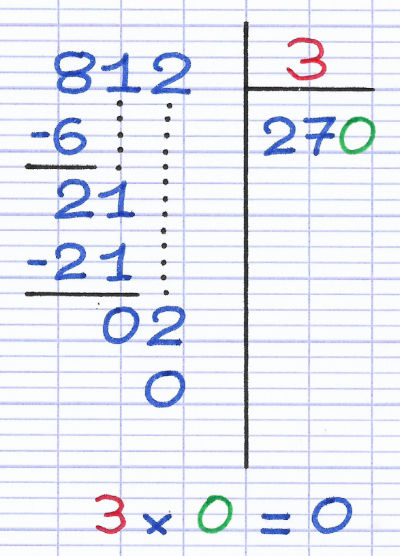
Le diviseur (3) est multiplié par le 3e chiffre du quotient (0).
On soustrait ensuite au reste provisoire (en rouge) le résultat de la multiplication (en vert). La réponse se note en-dessous de la soustraction.
C’est le reste final de la division euclidienne, car il n’y a plus de chiffre à descendre au niveau du dividende. Ce reste est toujours inférieur au diviseur (si ce n’est pas le cas, une erreur a été commise aux étapes précédentes).
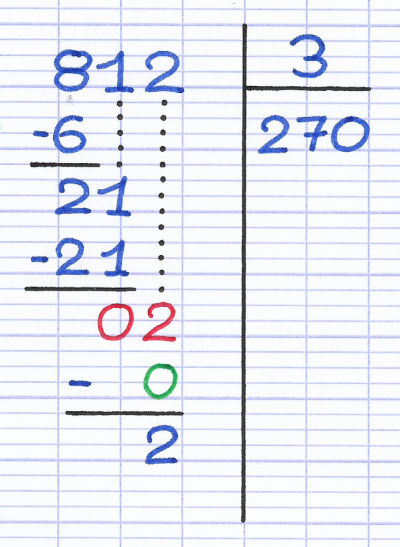
Soustraction du reste provisoire (2) par le résultat de la multiplication (0). La réponse (2) est le reste final de la division euclidienne. Le reste est inférieur au diviseur (2 < 3).
7. Trouver le Quotient et le Reste
Après avoir effectué la soustraction, s’il n’y a plus aucun chiffre du dividende à descendre, la division euclidienne est terminée :
- Le quotient (en rouge) est le nombre en bas de la droite horizontale.
- Le reste (en vert) est le nombre tout en bas à gauche de la droite verticale.
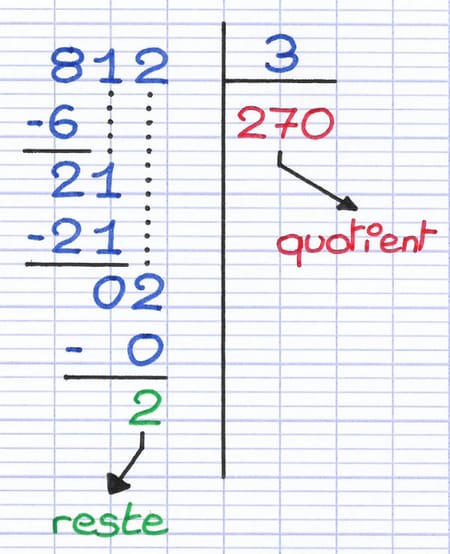
Le quotient de la division euclidienne est "270".
Le reste de la division euclidienne est "2".
Cas particuliers
La question de l’étape 2 (trouver le 1er chiffre du quotient) change dans certains cas particuliers. Si la réponse est "0", on repère les 2 premiers chiffres du dividende et on transforme légèrement la question : "Par combien faut-il multiplier le diviseur pour obtenir le plus grand nombre inférieur ou égal aux 2 premiers chiffres du dividende ?"
La réponse se note en-dessous de la droite horizontale, puis on effectue toutes les autres étapes normalement.
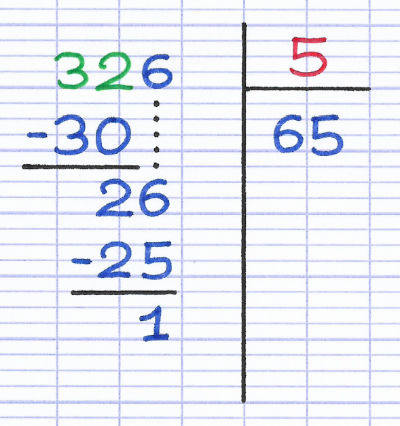
Le plus grand nombre inférieur ou égal à 32 est obtenu en multipliant le diviseur par 6 (5 x 6 = 30). Le 1er chiffre du quotient de la division euclidienne est donc 6.
Parfois, la réponse est encore "0" même avec les 2 premiers chiffres du dividende. Dans ce cas, on repère les 3 premiers chiffres du dividende et transforme à nouveau la question : "Par combien faut-il multiplier le diviseur pour obtenir le plus grand nombre inférieur ou égal aux 3 premiers chiffres du dividende ?"
La réponse se note en-dessous de la droite horizontale, puis on continue à effectuer toutes les autres étapes normalement.
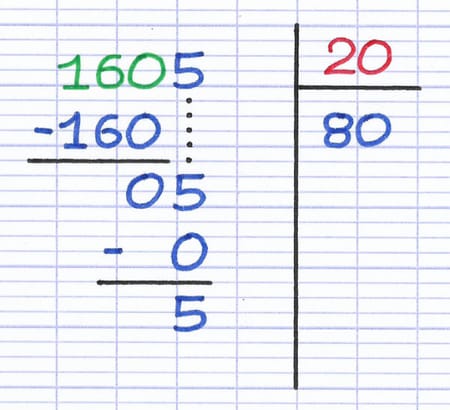
Le plus grand nombre inférieur ou égal à 160 est obtenu en multipliant le diviseur par 8 (20 x 8 = 160). Le 1er chiffre du quotient de la division euclidienne est donc 8.
En conclusion, on prend en considération un chiffre supplémentaire du dividende à chaque fois que la réponse à la question est "0".
Multiple et diviseur
La division euclidienne permet de trouver les multiples et diviseurs d’un nombre. Si le reste final d’une division euclidienne est "0", alors le dividende est un multiple du diviseur.

Le reste final de la division euclidienne est "0". Le dividende (224) est donc un multiple du diviseur (7).
Équation mathématique
Il existe une équation qui unit les 4 éléments de la division euclidienne. Le dividende est toujours égal au produit (multiplication) du diviseur par le quotient, auquel on ajoute le reste.
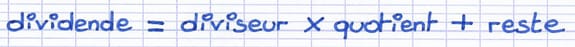
Cette équation mathématique unit le dividende, le diviseur, le quotient et le reste d’une division euclidienne.
Cette équation permet de vérifier que le quotient et le reste sont corrects :
- Si l’égalité est vraie, la division euclidienne est correcte.
- Si l’égalité est fausse, la division euclidienne contient une erreur.
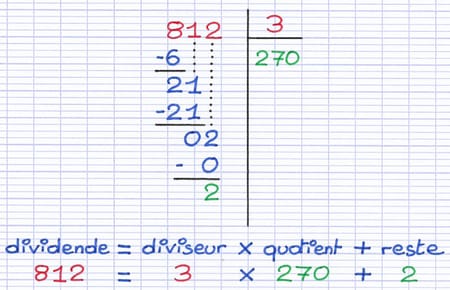
Le dividende (812) est égal au produit du diviseur (3) par le quotient (270) auquel on ajoute le reste (2). L’égalité est vraie, la division euclidienne est donc correcte.