Trouver les Multiples et Diviseurs d’un Nombre

🎯

Questions validées : 0 / 3

Théorie

En mathématiques, multiples et diviseurs sont liés par une propriété dans laquelle A et B représentent 2 nombres entiers.

Propriété : "Si A est un multiple de B, alors B est un diviseur de A".

Lien entre multiple et diviseur — **Multiple** et **diviseur** sont intimement liés.

Trouver les Multiples d’un Nombre

La technique pour trouver des multiples repose sur une propriété mathématique dans laquelle A, B et C sont des nombres entiers.

Propriété : "Si la multiplication de A par B est égale à C, alors C est un multiple de A et B".

Propriété mathématique pour trouver des multiples — La multiplication de 4 par 7 est égale à 28, donc 28 est un **multiple** de 4 et 7.

Tous les multiples d’un nombre se trouvent dans sa table de multiplication. On peut donc trouver rapidement des multiples d’un nombre en connaissant sa table de multiplication.

Table de multiplication pour trouver des multiples — Tous les multiples de 7 se trouvent dans la table de multiplication de 7.

**Multiples de 7** : 0, 7, 14, 21, 28... (la liste est infinie).

Fiche de Synthèse

Apprendre les Tables de Multiplication

Pour trouver les multiples d’un nombre dont on ne connait pas la table de multiplication, on peut procéder par calcul. Il suffit en effet de multiplier le nombre par n’importe quel nombre entier pour obtenir un multiple.

Trouver des multiples par multiplication — Chaque fois qu’on multiplie 15 par un nombre entier, on obtient un de ces multiples.

**Multiples de 15** : 30, 150, 1500,...

Trouver les Diviseurs d’un Nombre

La technique pour trouver des diviseurs repose sur une propriété mathématique dans laquelle A, B et C sont des nombres entiers.

Propriété : "Si la division de A par B est égale à C, alors B et C sont des diviseurs de A".

Propriété mathématique pour trouver des diviseurs — La division de 28 par 7 est égale à 4, donc 7 et 4 sont des **diviseurs** de 28.

Les tables de multiplication permettent de trouver tous les diviseurs d’un nombre. Il suffit pour cela de se demander dans quelles tables de multiplication se trouve le nombre dont on cherche les diviseurs. Chaque réponse est un diviseur du nombre.

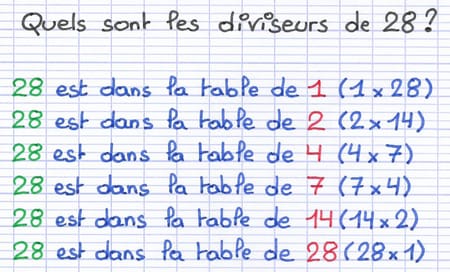
Table de multiplication pour trouver des diviseurs — 28 est dans la table de multiplication de 1, 2, 4, 7, 14 et 28.

Les **diviseurs de 28** sont donc 1, 2, 4, 7, 14 et 28.

Technique de Vérification

On peut vérifier facilement qu’un nombre est un multiple ou un diviseur à l’aide d’une division. Si la division de A par B est égale à un nombre entier, alors :

A est un multiple de B.
B est un diviseur de A.

Vérifier un multiple ou un diviseur avec une division — 28 est-il un **multiple de 7** ?

On vérifie que la division de 28 par 7 est égale à un nombre entier.

5 est-il un **diviseur de 28** ?

On vérifie que la division de 28 par 5 est égale à un nombre entier.

La vérification peut s’effectuer à l’aide d’une division euclidienne. Si le reste de la division euclidienne de A par B est 0, alors :

A est un multiple de B.
B est un diviseur de A.

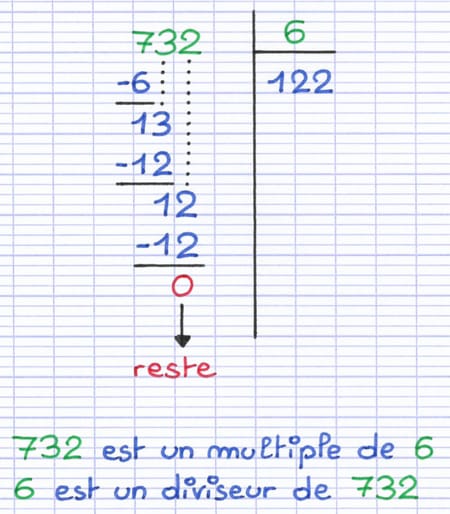
Division euclidienne pour vérifier un multiple ou diviseur — 732 est-il un multiple de 6 ? 6 est-il un diviseur de 732 ? Oui, car le reste de la **division euclidienne** de 732 par 6 est 0.

Fiche de Synthèse

Effectuer une Division Euclidienne avec Reste

Les critères de divisibilité permettent également de vérifier qu’un nombre est un multiple ou un diviseur. Si A satisfait au critère de divisibilité par B, alors :

A est un multiple de B.
B est un diviseur de A.

Critères de divisibilité pour vérifier un multiple ou diviseur — Le **critère de divisibilité par 5** permet de vérifier qu’un nombre est divisible par 5 ou est multiple de 5. Les multiples de 5 se terminent par 0 ou 5. Les nombres entiers qui se terminent par 0 ou 5 ont comme diviseur 5.

Fiche de Synthèse

Utiliser les Critères de Divisibilité

Cas Particuliers

Tous les nombres entiers, à l’exception de zéro, possèdent une infinité de multiples. Zéro est le seul nombre entier qui ne possède qu’un seul multiple : lui-même (zéro).

0 est le seul multiple de zéro — La multiplication de 0 par un nombre est toujours égale à 0. Le seul multiple de zéro est 0.

Zéro possède un seul multiple, mais il est le multiple de tous les nombres entiers. Zéro n’est par contre le diviseur d’aucun nombre, car il est impossible de diviser un nombre par zéro.

Zéro est le multiple de tous les nombres entiers — Si on multiplie n’importe quel nombre par 0, on obtient 0. 0 est donc le multiple de n’importe quel nombre (1, 2, 3...).

Tous les nombres entiers sont dans la table de multiplication de 1, donc tous les nombres sont des multiples de 1. 1 est également le diviseur de tous les nombres entiers, car tous les nombres sont divisibles par 1.