Identifier les Polygones avec un Centre de Symétrie

Apprenez la Théorie puis affrontez notre Quiz

Théorie

Certains polygones (ou figures géométriques) particuliers possèdent un centre de symétrie. Les polygones qui possèdent un centre de symétrie possèdent tous un nombre pair de sommets. Cependant, les polygones qui ont un nombre pair de sommets n’ont pas tous un centre de symétrie. Pour trouver le centre de symétrie d’un polygone, on cherche le point d’intersection de droites particulières.

Parallélogramme

Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles et de même longueur.

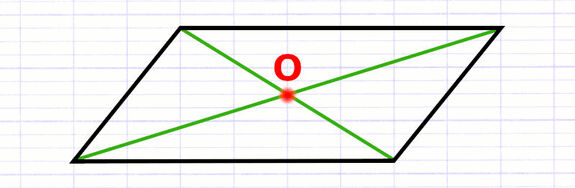
Le centre de symétrie du parallélogramme est le point d’intersection de ses diagonales. Une diagonale est une droite qui relie 2 sommets non consécutifs d’un polygone.

Propriété : "Tous les quadrilatères qui possèdent un centre de symétrie sont des parallélogrammes".

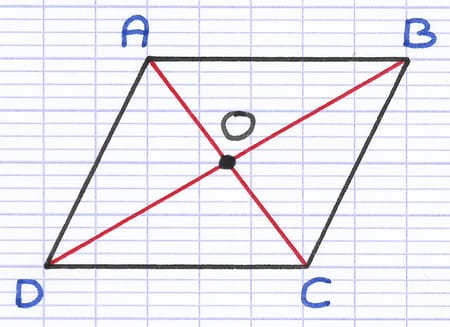
Parallélogramme ABCD avec son centre de symétrie correspondant au point d’intersection de ses diagonales [AC] et [BD]. — (AC) et (BD) sont les diagonales du parallélogramme. Le point O est le **centre de symétrie** du parallélogramme.

Losange

Un losange est un parallélogramme dont tous les côtés sont de même longueur.

Le centre de symétrie du losange est le point d’intersection de ses diagonales.

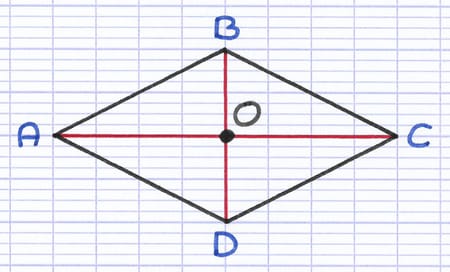
Losange ABCD avec son centre de symétrie correspondant au point d’intersection de ses diagonales [AC] et [BD]. — (AC) et (BD) sont les diagonales du losange. Le point O est le **centre de symétrie** du losange.

Rectangle

Un rectangle est un parallélogramme dont tous les angles sont des angles droits (90°).

Le centre de symétrie du rectangle est le point d’intersection de ses diagonales et médiatrices. Une médiatrice est une droite qui passe par le milieu d’un segment et qui est perpendiculaire à ce segment.

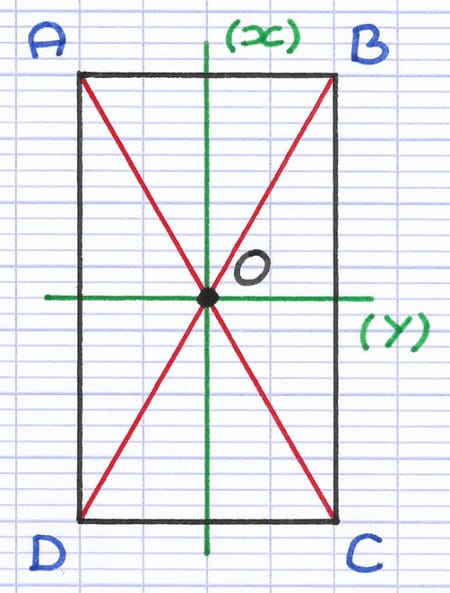
Rectangle ABCD avec son centre de symétrie correspondant au point d’intersection de ses diagonales [AC] et [BD]. — En rouge, (AC) et (BD) sont les diagonales du rectangle. En vert, (x) et (y) sont les médiatrices du rectangle. Le point O est le **centre de symétrie** du rectangle.

Carré

Un carré est un parallélogramme possédant à la fois les caractéristiques du losange et du rectangle.

Le centre de symétrie du carré est le point d’intersection de ses diagonales et médiatrices.

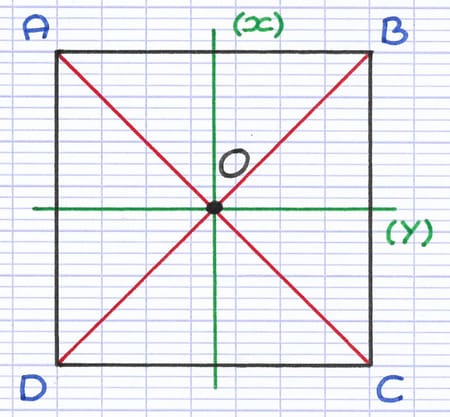
Carré ABCD avec son centre de symétrie correspondant au point d’intersection de ses diagonales [AC] et [BD]. — En rouge, (AC) et (BD) sont les diagonales du carré. En vert, (x) et (y) sont les médiatrices du carré. Le point O est le **centre de symétrie** du carré.

Hexagone Régulier

Un hexagone régulier est un polygone à 6 côtés de même mesure.

Le centre de symétrie de l’hexagone régulier est le point d’intersection de ses diagonales.

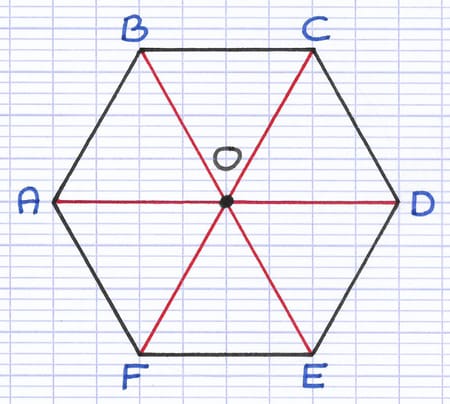
Hexagone régulier ABCDEF avec son centre de symétrie correspondant au point d’intersection de ses diagonales [AD], [BE] et [CF]. — [AD], [BE] et [CF] sont les diagonales qui relient les sommets opposés. Le point O est le **centre de symétrie** de l’hexagone régulier.

Cercle

Un cercle est une figure géométrique constituée d’une ligne courbe fermée.

Le centre de symétrie du cercle correspond au centre du cercle (point d’intersection des diamètres).

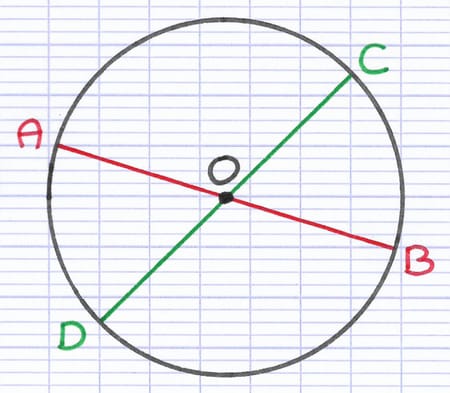
Cercle avec son centre de symétrie correspondant au point d’intersection des diamètres [AB] et [CD]. — [AB] et [CD] sont des diamètres du cercle. Le centre O est le **centre de symétrie** du cercle.

★

Polygones sans centre de symétrie

★

Certains polygones particuliers ne possèdent aucun centre de symétrie. C’est notamment le cas du triangle et du trapèze.

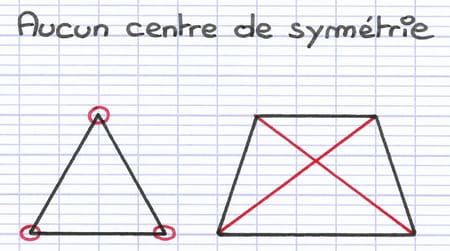
Triangle et trapèze, deux figures qui ne possèdent pas de centre de symétrie. — Le triangle possède un nombre impair de sommets. Le point d’intersection des diagonales du trapèze n’est pas un centre de symétrie.

à propos de l’auteur

Benoit Baudoin

Professeur particulier de mathématiques

Envie de progresser ? Contactez-moi sur WhatsApp pour recevoir des cours particuliers en ligne.

+372 5899 6405

Quiz

espace membre

Connectez-vous à votre espace membre pour affronter nos exercices

Inscription Connexion

Question 1

Exercice 1 : Identifier les polygones avec un centre de symétrie

Cette illustration est composée de trois polygones : un trapèze, un triangle et un rectangle. Combien de ces polygones possèdent un centre de symétrie ?

Question 2

Exercice 2 : Identifier les polygones avec un centre de symétrie

Laquelle de ces propriétés relatives aux quadrilatères est vraie ?

Question 3

Laquelle de ces propositions est fausse ?