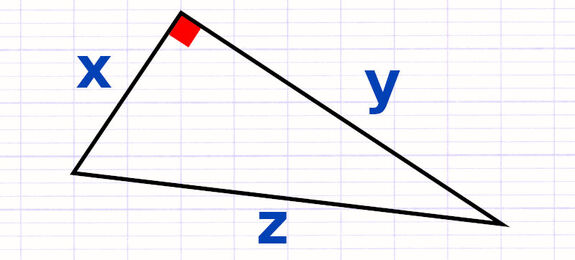
Mettre en Équation le Théorème de Pythagore
Théorie
Théorème de Pythagore : "Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des 2 autres côtés".
La mise en équation du théorème de Pythagore consiste à transformer l’énoncé en une formule mathématique.
Mise en équation
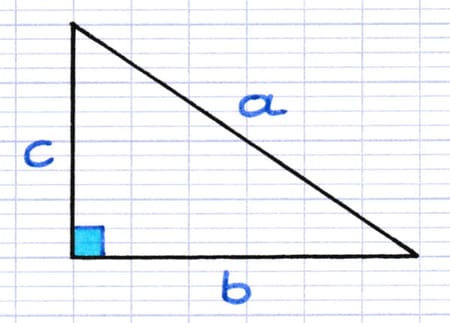
Comment mettre en équation le théorème de Pythagore à partir de ce triangle rectangle ?
Le Carré de la Longueur de l’Hypoténuse...
L’énoncé du théorème de Pythagore commence par "Le carré de la longueur de l’hypoténuse..."
La 1re étape est d’identifier la longueur de l’hypoténuse au sein du triangle rectangle. Dans un triangle rectangle, l’hypoténuse est le côté opposé à l’angle droit (en face).
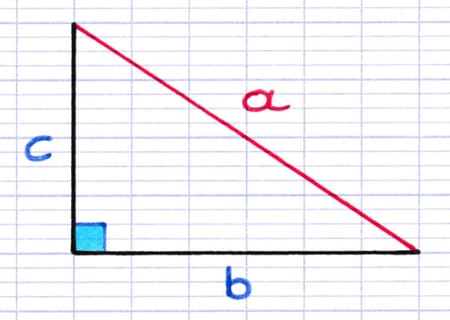
L’hypoténuse (en rouge) est le seul côté qui ne touche pas le sommet de l’angle droit. La longueur de l’hypoténuse est indiquée par la lettre "a".
Une fois la longueur de l’hypoténuse identifiée, on peut écrire "Le carré de la longueur de l’hypoténuse" sous forme d’une équation. Si la longueur de l’hypoténuse est "a", alors le carré de la longueur de l’hypoténuse est "a²".
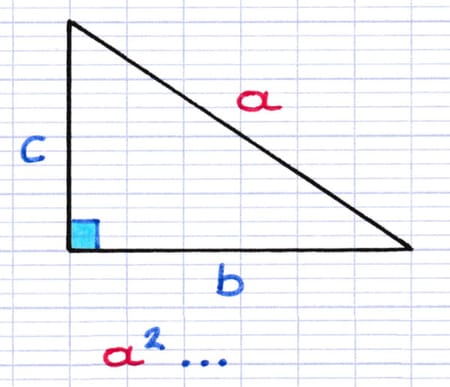
Théorème : Le carré de la longueur de l’hypoténuse ...
Équation : a2 ...
... Est Égal à ...
L’énoncé du théorème de Pythagore se poursuit par "... est égal à ..."
Au sein d’une formule mathématique, une égalité est symbolisée par le signe égal (=). L’étape suivante est donc d’écrire le signe égal à la suite de l’équation.
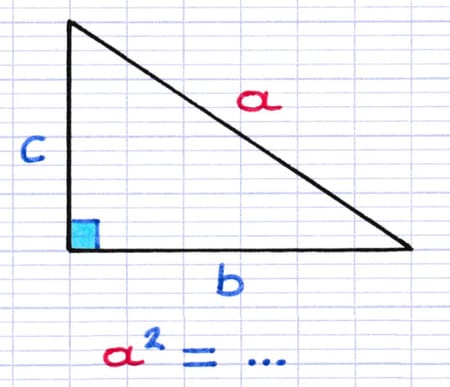
Théorème : Le carré de la longueur de l’hypoténuse est égal à ...
Équation : a2 = ...
... La Somme des Carrés des Longueurs des 2 Autres Côtés
L’énoncé du théorème de Pythagore se termine par "... la somme des carrés des longueurs des 2 autres côtés".
La dernière étape est d’identifier la longueur de ces 2 autres côtés. Il s’agit des 2 côtés du triangle rectangle qui forment l’angle droit.
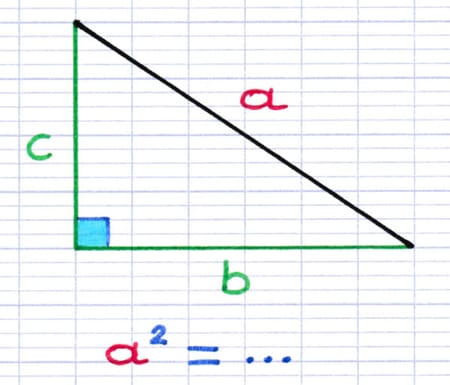
Les 2 autres côtés (en vert) sont les 2 côtés de l’angle droit. Leur longueur est indiquée par les lettres "b" et "c".
Une fois la longueur des 2 autres côtés identifiée, on peut écrire "la somme des carrés des longueurs des 2 autres côtés" sous forme d’une équation. Au sein d’une formule mathématique, une somme est symbolisée par le signe de l’addition (+). Si les longueurs des 2 autres côtés sont "b" et "c", alors les carrés des longueurs sont "b²" et "c²".
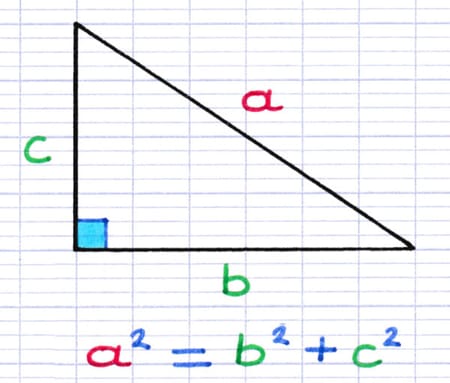
Théorème : Le carré de la longueur de l’hypoténuse est égal à la somme des carrés des 2 autres côtés.
Équation : a2 = b2 + c2.
Dans ce triangle rectangle, le résultat de la mise en équation du théorème de Pythagore est "a² = b² + c²".
Cas particulier
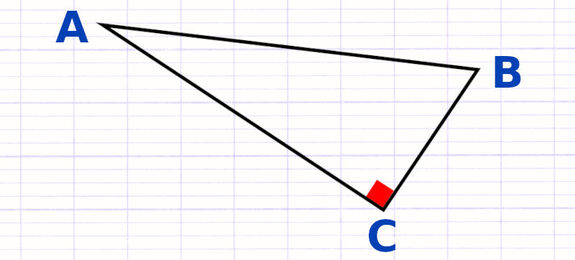
Dans certains triangles rectangles, aucune lettre minuscule n’indique la longueur des côtés. Dans ce cas, on indique la longueur des côtés en utilisant les lettres majuscules des différents sommets.
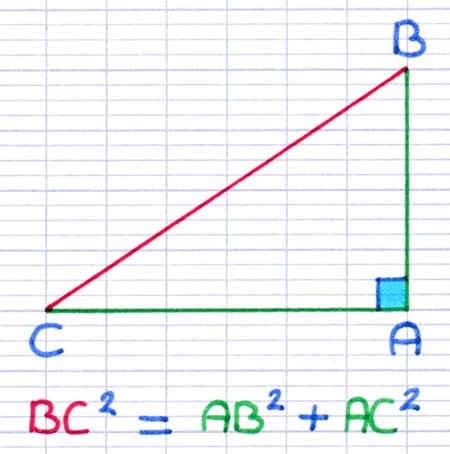
La longueur de l’hypoténuse (en rouge) est BC.
La longueur des 2 autres côtés (en vert) est AB et AC.
Équation de Pythagore : BC2 = AB2 + AC2.
Dans ce triangle rectangle, la mise en équation du théorème de Pythagore est "BC² = AB² + AC²".