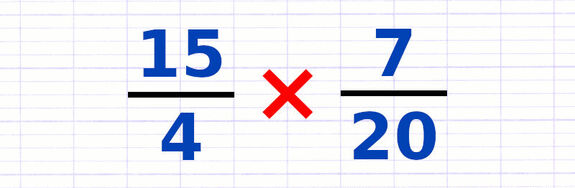
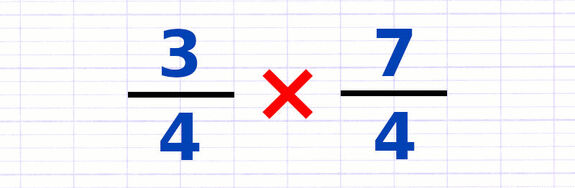
Multiplier des Fractions
Théorie
La multiplication de fractions s’effectue en multipliant séparément les numérateurs et les dénominateurs. Contrairement à l’addition et la soustraction, il n’est pas nécessaire de placer les fractions sur un dénominateur commun.
Exemple
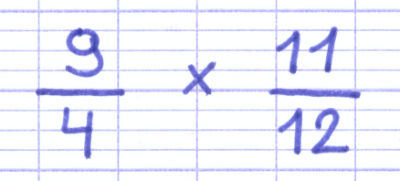
Comment multiplier les fractions 9/4 et 11/12 ?
Simplifier les Fractions
La 1re étape est de simplifier, lorsque c’est possible, les fractions à multiplier. La simplification s’effectue en divisant un numérateur et un dénominateur par leur plus grand commun diviseur (PGCD). Au sein d’une multiplication, il est possible de simplifier le numérateur d’une fraction avec le dénominateur d’une autre fraction.
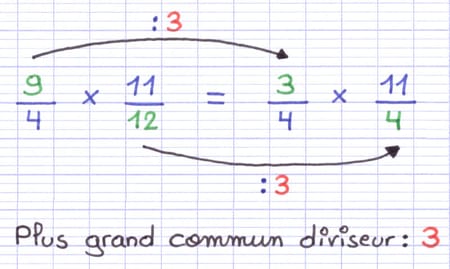
Il est possible de diviser le numérateur de la 1re fraction (9) et le dénominateur de la 2e fraction (12) par un diviseur commun (3). Multiplier 9/4 par 11/12 est équivalent à multiplier 3/4 par 11/4.
Multiplier Numérateurs et Dénominateurs
La multiplication de fractions s’effectue en séparant les numérateurs et les dénominateurs :
- Les numérateurs sont multipliés entre eux.
- Les dénominateurs sont multipliés entre eux.
On multiplie les numérateurs entre eux (3 x 11 = 33) et les dénominateurs entre eux (4 x 4 = 16). Le résultat de la multiplication est la fraction 33/16.
Simplifier le Résultat
La dernière étape est de s’assurer que la réponse obtenue est une fraction irréductible (simplifiée au maximum). Si le résultat est une fraction irréductible, l’exercice est terminé. Sinon, la fraction doit être simplifiée.
Le seul diviseur commun entre le numérateur (33) et le dénominateur (16) est le chiffre 1. 33/16 est une fraction irréductible, il s’agit de la réponse finale.
Quiz
Question 1
Quelle est la première étape recommandée pour multiplier ces deux fractions ?
Question 2
Laquelle de ces affirmations est fausse dans le cadre d’une multiplication de deux fractions ?
Question 3
Quel est le résultat de la multiplication de ces deux fractions ?