Reconnaître les Carrés Parfaits
Théorie
Un carré parfait est le résultat d’un nombre entier multiplié par lui-même.

4, 49 et 10 000 sont des carrés parfaits.
La multiplication d’un nombre par lui-même peut s’écrire sous la forme d’une puissance. Un carré parfait est le résultat d’une puissance dont :
- La base est un nombre entier.
- L’exposant est 2.
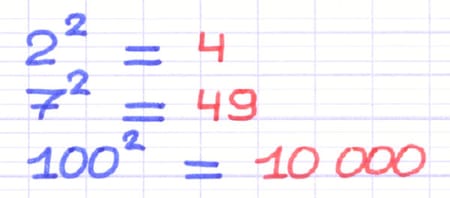
22 = 2 x 2 = 4
72 = 7 x 7 = 49
1002 = 100 x 100 = 10 000
Chaque carré parfait est l’aire d’un carré dont la longueur des côtés est un nombre entier. Il est donc possible de représenter un carré parfait par une forme géométrique carrée.
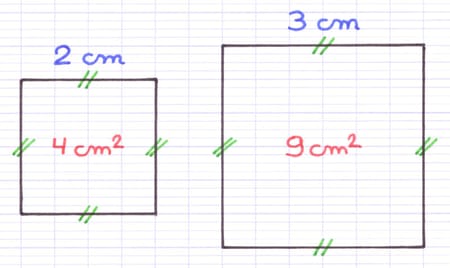
Le carré parfait 4 est l’aire d’un carré de côté 2 cm.
Le carré parfait 9 est l’aire d’un carré de côté 3 cm.
Il y a un nombre infini de carrés parfaits. En Quatrième, il faut connaître tous les carrés parfaits compris entre 1 et 144.

Les carrés parfaits de 1 à 144 classés par ordre croissant : 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121 et 144.
On peut déterminer si un nombre est un carré parfait à l’aide d’un calcul. Il suffit de vérifier si on peut obtenir ce nombre en multipliant un nombre entier par lui-même.

Il est impossible d’obtenir 32 en multipliant un nombre entier par lui-même. 32 n’est donc pas un carré parfait.
Le dernier chiffre de tous les carrés parfaits est 0, 1, 4, 5, 6 ou 9. Un nombre qui se termine par 2, 3, 7 ou 8 n’est donc jamais un carré parfait.
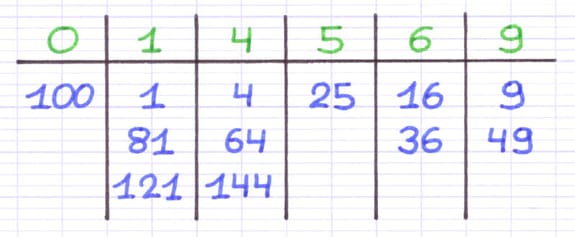
Un carré parfait se termine toujours par 0, 1, 4, 5, 6 ou 9.
