Reconnaître et Décrire un Pavé Droit
Théorie
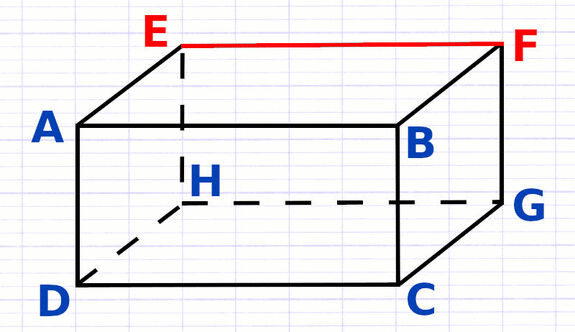
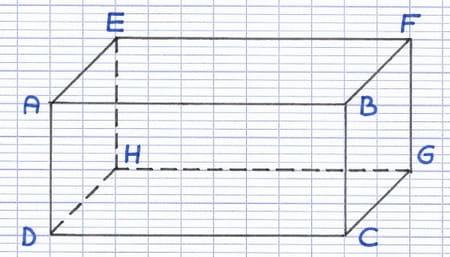
Le pavé droit (ou parallélépipède rectangle) est un solide polyèdre dont les 6 faces sont des rectangles. En perspective cavalière, seuls les faces avant et arrière du pavé droit sont représentées en vraie grandeur. Les autres faces sont déformées (les angles droits apparaissent aigus ou obtus).
La caractéristique du pavé droit est de posséder 6 faces rectangulaires.
Sommets
Le pavé droit possède 8 sommets, qui correspondent aux différents coins de la figure. Le nom du parallélépipède rectangle est composé de ses sommets classés par ordre alphabétique.
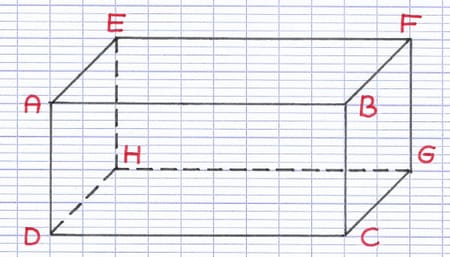
Tous les pavés droits possèdent 8 sommets. Le nom de ce parallélépipède rectangle est ABCDEFGH.
Arêtes
Le pavé droit possède 12 arêtes, qui correspondent aux différents segments de la figure. Toutes les arêtes parallèles ont la même longueur.
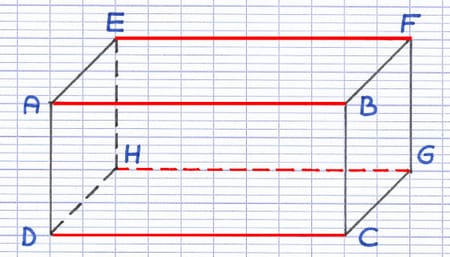
[AB], [DC], [EF] et [HG] sont parallèles.
AB = DC = EF = HG (même longueur).
Toutes les arêtes issues d’un même sommet sont perpendiculaires.
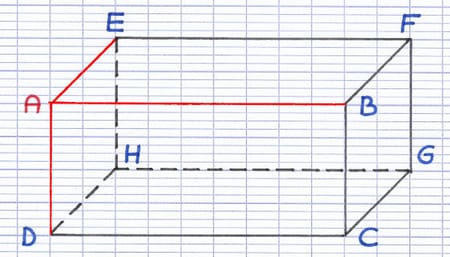
[AB], [AE] et [AD] sont issus du même sommet A.
[AB], [AE] et [AD] sont perpendiculaires.
Faces
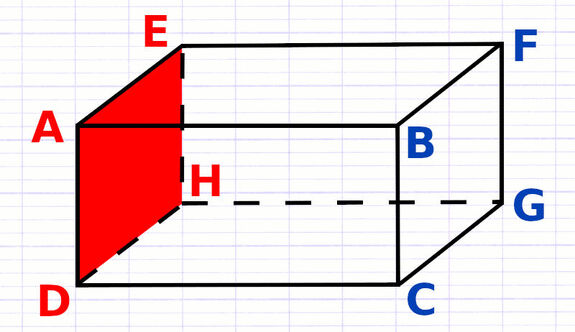
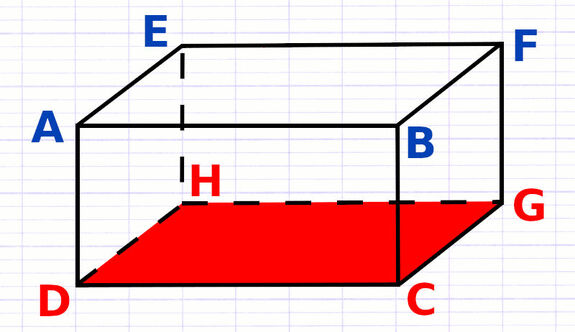
Le pavé droit possède 6 faces, qui correspondent aux surfaces planes (2D) délimitées par ses arêtes. Toutes les faces opposées sont parallèles.
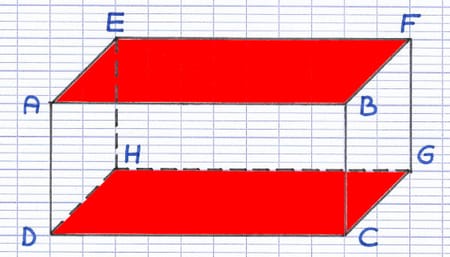
Les faces opposées n’ont pas d’arête commune, elles sont face à face. AEFB et DHGC sont des faces opposées parallèles.
Toutes les faces non opposées sont perpendiculaires.
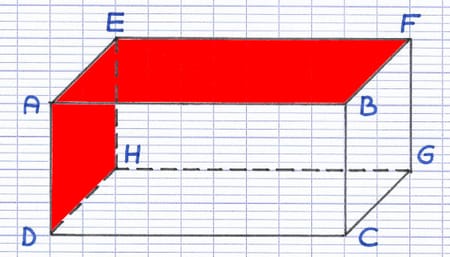
Les faces non opposées ont une arête commune, elles se touchent. AEFB et AEHD sont des faces non opposées perpendiculaires.
Exercices
Question 1
Quelles sont les arêtes perpendiculaires à [EF] ?
Question 2
Quelle face est parallèle à la face AEHD ?
Question 3
Combien de faces sont perpendiculaires à la face DHGC ?