Reconnaître et Décrire un Quadrilatère
Théorie
Un quadrilatère est un polygone à 4 côtés. Tous les quadrilatères partagent des caractéristiques communes.
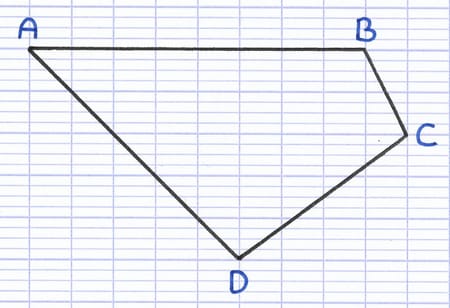
ABCD est un quadrilatère.
4 Côtés
La caractéristique principale du quadrilatère est de posséder 4 côtés :
- 2 côtés sont consécutifs s’ils partagent un sommet commun (les côtés se touchent en un point).
- 2 côtés sont opposés s’ils ne partagent pas de sommet commun (les côtés ne se touchent pas).
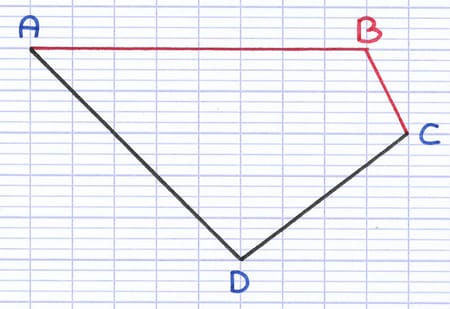
[AB], [BC], [CD] et [DA] sont les 4 côtés de ce quadrilatère.
Les côtés [AB] et [BC] sont consécutifs, leur sommet commun est B.
Les côtés [AB] et [CD] sont opposés, ils n’ont pas de sommet commun.
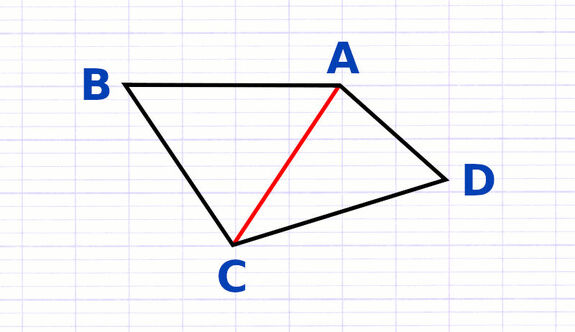
2 Diagonales
Les diagonales sont les segments qui relient 2 sommets opposés (2 sommets qui ne se suivent pas). Tous les quadrilatères possèdent 2 diagonales.
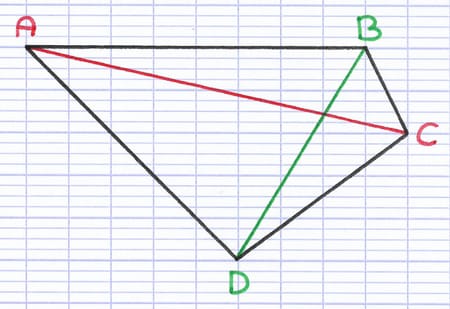
Les sommets A et C sont opposés, le segment [AC] est une diagonale.
Les sommets B et D sont opposés, le segment [BD] est une diagonale.
4 angles
Un angle est formé de 2 côtés qui partagent un sommet commun. Tous les quadrilatères possèdent 4 angles. La somme des 4 angles d’un quadrilatère est toujours de 360°.
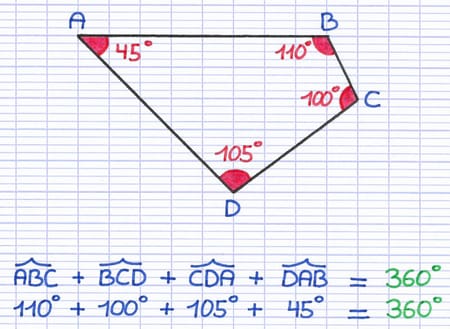
Ce quadrilatère possède 4 angles : ABC, BCD, CDA et DAB. L’addition des 4 angles est de 360°.
Quadrilatères particuliers
Certains quadrilatères possèdent des particularités supplémentaires qui les distinguent des autres:
- Le parallélogramme possède des côtés opposés parallèles et de même longueur.
- Le losange possède 4 côtés de même longueur.
- Le rectangle possède 4 angles droits.
- Le carré possède à la fois les caractéristiques du rectangle et du losange.
Exercice
Question 1
Cette figure représente-t-elle un quadrilatère ?
Question 2
Dans ce quadrilatère, quel est le nom du côté opposé au côté [AB] ?
Question 3
Que désigne le segment [AC] au sein de ce quadrilatère ?