Reconnaître la Configuration Emboîtée de Thalès
Théorie
Situation de Thalès
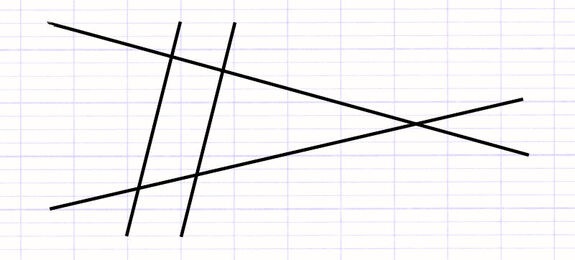
Le théorème de Thalès s’applique en présence d’une situation de Thalès (ou configuration de Thalès). Une situation de Thalès apparaît lorsque 2 droites sécantes sont coupées par 2 droites parallèles.
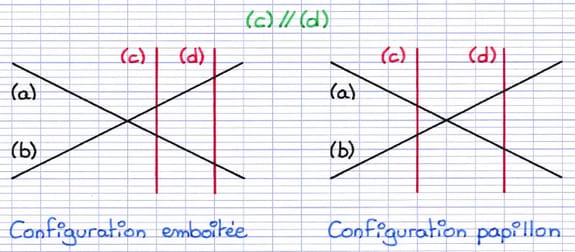
On parle de configuration "emboîtée" si les parallèles sont situées du même côté du point d’intersection des sécantes (configuration enseignée en Quatrième).
On parle de configuration "papillon" si les parallèles sont situées de part et d’autre du point d’intersection des sécantes (configuration enseignée en Troisième).
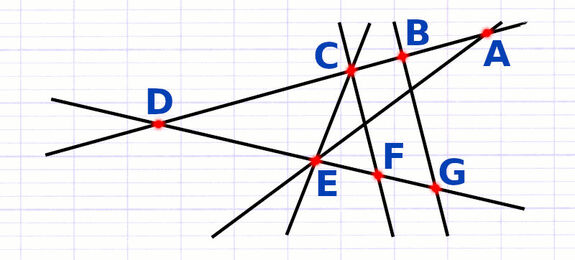
(a) et (b) sont 2 droites sécantes coupées par 2 droites parallèles (c) et (d). La position des parallèles fait apparaître une configuration de Thalès emboîtée ou papillon.
Configuration Emboîtée
En observant attentivement 2 sécantes coupées par 2 parallèles, on peut voir apparaître 2 triangles. Ces 2 triangles sont en situation de Thalès "emboîtée" si les parallèles sont situées du même côté du point d’intersection des sécantes. La situation de Thalès est dite "emboîtée" car un petit triangle est à l’intérieur d’un grand triangle.
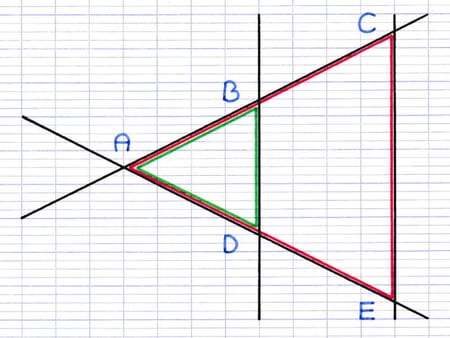
ACE et ABD sont 2 triangles en situation de Thalès emboîtée : ABD est emboîté dans ACE.
Caractéristiques
On peut reconnaître facilement 2 triangles en situation de Thalès "emboîtée" à l’aide de 3 caractéristiques :
- Les 2 triangles ont un sommet commun.
- Les 2 autres sommets du petit triangle sont situés sur les côtés du grand triangle.
- Les 2 côtés opposés au sommet commun sont parallèles.
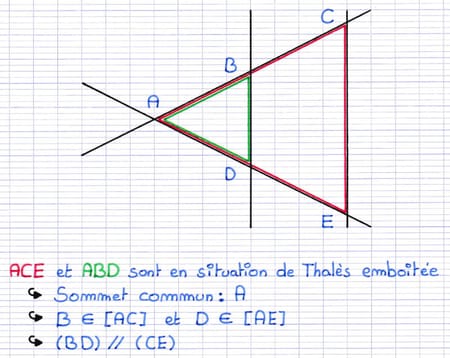
Caractéristiques permettant de reconnaître des triangles en situation de Thalès emboîtée.
Exercice
Question 1
Comment se nomme la configuration de Thalès ci-dessus ?
Question 2
Laquelle de ces propositions n’est pas une caractéristique de deux triangles en situation de Thalès emboîtée ?
Question 3
Sur cette figure, les points A, B, C, D sont alignés, ainsi que les points G, F, E et D. les droites (CF) et (BG) sont parallèles. Quels sont les deux triangles en situation de Thalès ?