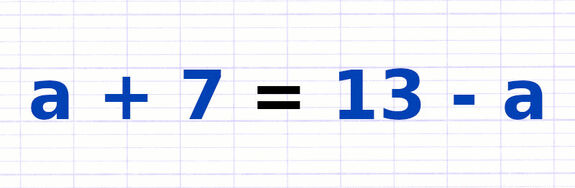Tester l'Égalité d'une Équation pour une Valeur Numérique
Une équation est une relation d'égalité entre 2 membres séparés par un signe "=".
Chaque membre d'une équation est composé de nombres et/ou de lettres.
Il est possible de tester l'égalité d'une équation pour n'importe quelle valeur numérique.
La technique consiste à remplacer les lettres par la valeur que l'on souhaite tester, et à effectuer ensuite les opérations.
-
1
Remplacer la lettre par sa valeur numérique
Une équation est toujours composée d'au moins une lettre.
Pour tester l'égalité d'une équation, la lettre doit être remplacée par une valeur numérique.
Dans ce type d'exercice, la valeur à tester est directement donnée dans l'énoncé.
La 1ère étape est de remplacer, dans chaque membre, la lettre par sa valeur.
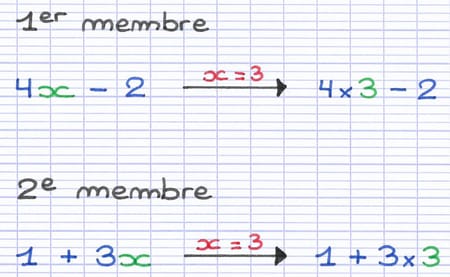
Dans chaque membre, la lettre (x) est remplacée par la valeur à tester (3).Un nombre collé à une lettre est équivalent à une multiplication. -
2
Effectuer les opérations
Chaque membre de l'équation est maintenant composé uniquement de nombres, on peut effectuer les opérations.
Lorsque tu calcules, n'oublie pas de respecter la règle de la priorité des opérations.
Fiche de SynthèseDéterminer l'ordre de priorité des opérations (PEMDAS)
Les opérations sont effectuées dans chaque membre séparément.La multiplication est prioritaire sur l'addition (PEMDAS). -
3
Comparer les résultats
Après avoir effectué toutes les opérations, tu obtiens un résultat pour chaque membre.
La comparaison de ces résultats détermine si l'égalité testée est vraie ou fausse:
- L'égalité est vraie si les résultats sont identiques.
- L'égalité est fausse si les résultats sont différents.
Les résultats des 2 membres de l'équation sont comparativement identiques (10).L'égalité est donc vraie pour "x = 3".
Vérifiez si votre puissance mathématique a augmenté !
Testez l'égalité de cette équation pour différentes valeurs numériques, puis comparez votre réponse avec la correction.
