Tracer l'Arbre de Probabilité d'une Expérience Aléatoire
L'arbre de probabilité est également appelé l'arbre des possibles ou l'arbre des issues.
Sa construction permet de visualiser la probabilité de chaque issue d'une expérience aléatoire.
-
1
Identifier les issues de l'expérience
La 1ère étape est d'identifier les différentes issues de l'expérience aléatoire.
Lorsqu'on lance une pièce de monnaie, il y a 2 issues possibles: pile ou face.
Le symbole Ω désigne l'ensemble des issues d'une expérience aléatoire. -
2
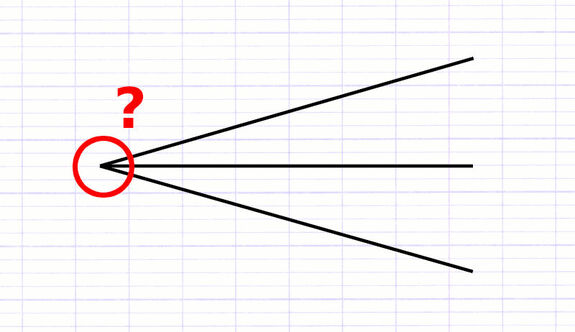
Construire les branches de l'arbre
À partir d'un même point d'origine (appelé racine), trace une branche pour chacune des issues.
Chaque branche de l'arbre mène à une issue différente de l'expérience aléatoire.
Chacune des issues est indiquée à l'extrémité droite d'une branche.
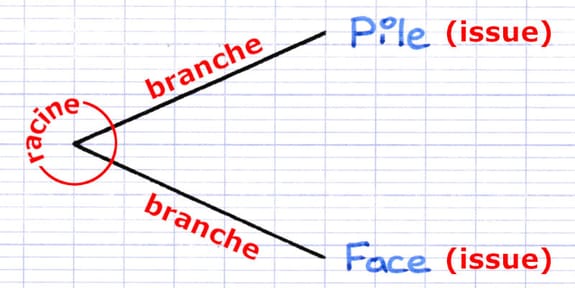
La racine (origine) de l'arbre de probabilité est située à gauche.À partir de la racine, chaque branche mène à une issue différente.On se déplace donc dans un arbre de probabilité de gauche à droite. -
3
Pondérer l'arbre de probabilité
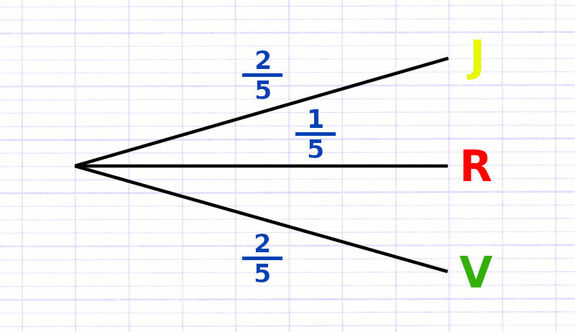
Complète ensuite l'arbre en indiquant sur chaque branche la probabilité de l'issue correspondant.
La probabilité peut s'écrire sous la forme d'une fraction, d'un nombre décimal ou d'un pourcentage.
La pièce de monnaie n'étant pas truquée, il y 1 chance sur 2 d'obtenir chaque issue.
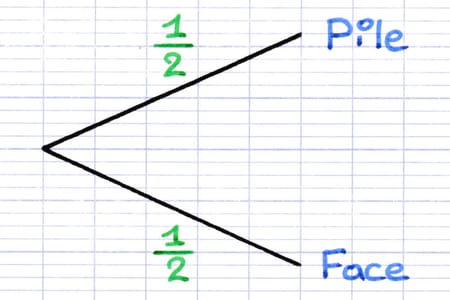
Lorsque les probabilités figurent sur les branches, on parle d'arbre de probabilité pondéré. Propriété: La somme des probabilités de toutes les issues d'une expérience aléatoire est égale à 1.
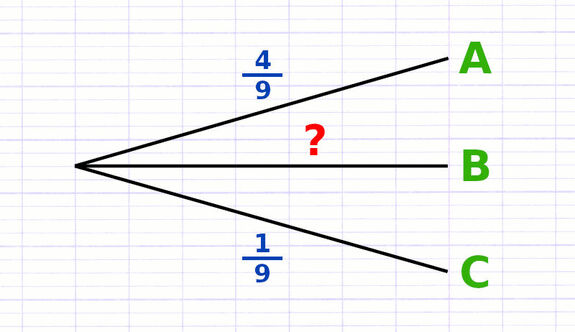
Sers-toi de cette propriété pour vérifier que tu n'as pas fait d'erreur !
Dans un arbre de probabilité, la somme des probabilités des branches émanant de la racine est toujours égale à 1.
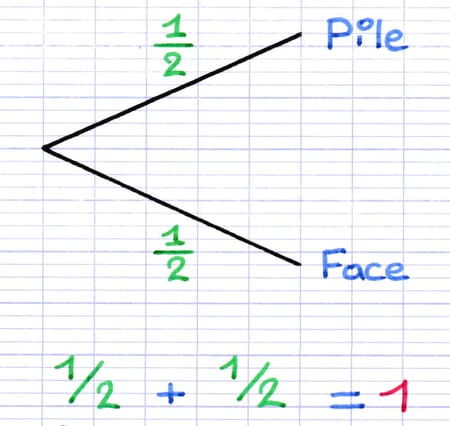
La somme des probabilités de toutes les branches est égale à 1.
Vérifiez si votre puissance mathématique a augmenté !
Expérience: Je tire au hasard une boule du sac ci-dessous et je note sa couleur.
Tracez l'arbre de probabilité de cette expérience aléatoire, puis comparez votre réponse avec la correction.
