Tracer les Hauteurs d’un Triangle
Théorie
Dans un triangle, une hauteur est une droite perpendiculaire à un côté et qui passe par le sommet opposé. Tous les triangles possèdent 3 hauteurs (une hauteur par côté).
Triangle Quelconque
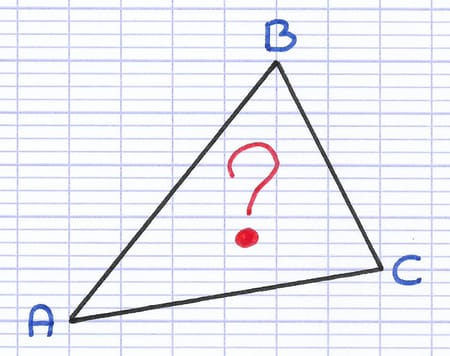
Comment tracer les hauteurs de ce triangle quelconque ?
Pour tracer une hauteur au sein d’un triangle quelconque, on choisit l’un de ses côtés. La technique consiste à tracer une droite perpendiculaire au côté choisi, en veillant à ce que la droite passe par le sommet opposé. Le sommet opposé est le sommet en face du côté choisi (le seul sommet qui ne touche pas le côté).
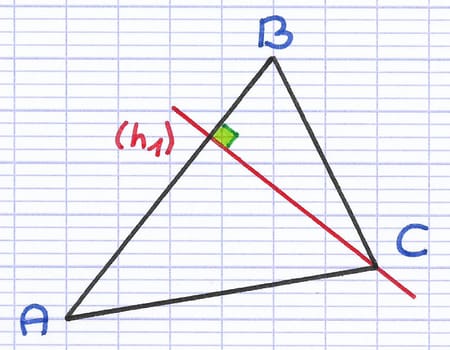
La droite (h1) est une hauteur du triangle. La droite est perpendiculaire au côté [AB] et passe par le sommet opposé C.
Pour construire toutes les hauteurs du triangle, il suffit de répéter la procédure à partir des deux autres côtés.
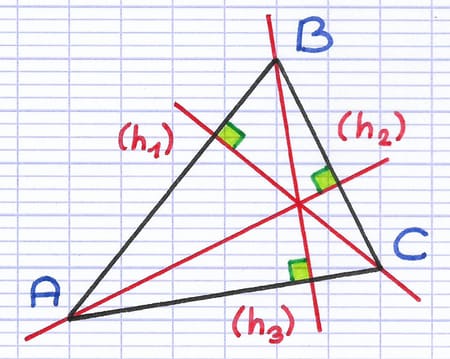
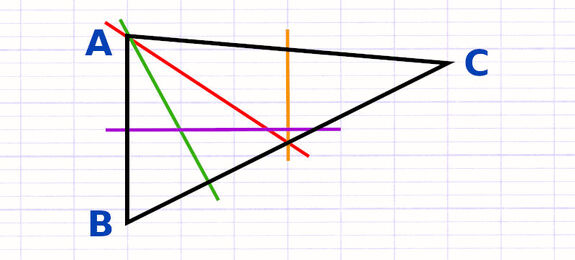
Les droites (h1), (h2) et (h3) sont les 3 hauteurs du triangle.
Triangle Rectangle
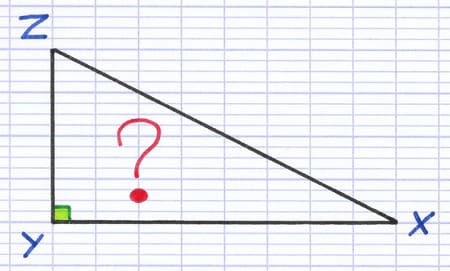
Comment tracer les hauteurs de ce triangle rectangle ?
Un triangle rectangle a la particularité de posséder un angle droit (90°), et donc 2 côtés perpendiculaires. Lorsqu’on trace la hauteur issue de chacun de ces 2 côtés perpendiculaires, on se rend compte que la hauteur se superpose sur l’autre côté. Un triangle rectangle possède donc 2 hauteurs qui correspondent exactement aux 2 côtés de l’angle droit.
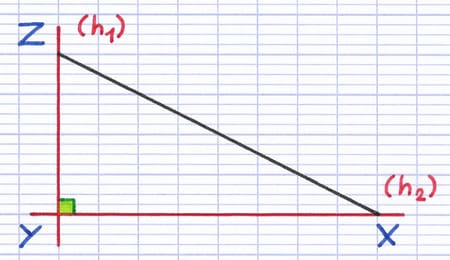
La hauteur (h1) issue du côté [XY] se superpose sur le côté [YZ].
La hauteur (h2) issue du côté [YZ] se superpose sur le côté [XY].
La 3e hauteur du triangle rectangle issue de l’hypoténuse (côté opposé à l’angle droit) n’a rien de particulier. Le point d’intersection des hauteurs du triangle rectangle (orthocentre) correspond au sommet de l’angle droit.
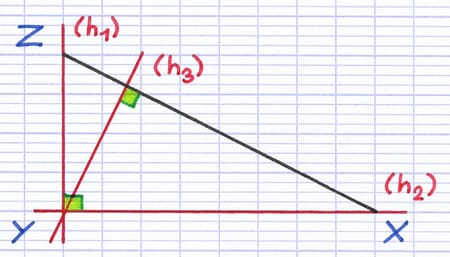
Les droites (h1), (h2) et (h3) sont les 3 hauteurs du triangle rectangle.
Triangle Obtusangle
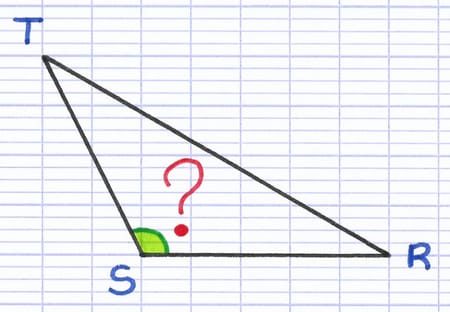
Comment tracer les hauteurs de ce triangle obtusangle ?
Un triangle obtusangle a la particularité de posséder un angle obtus. Lorsqu’on trace la hauteur issue de chacun des 2 côtés de l’angle obtus, on se rend compte que la hauteur est à l’extérieur du triangle. En effet, on est obligé de prolonger les côtés de l’angle obtus pour tracer les perpendiculaires.
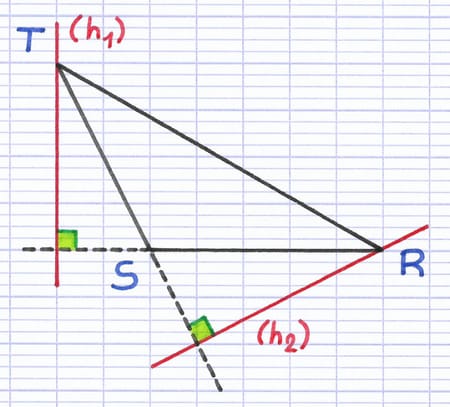
Un triangle obtusangle possède 2 hauteurs à l’extérieur.
La 3e hauteur du triangle obtusangle n’a rien de particulier.
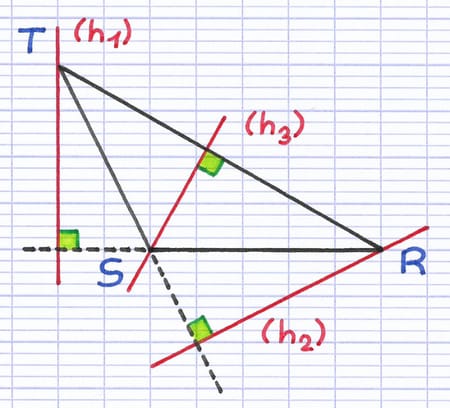
Les droites (h1), (h2) et (h3) sont les 3 hauteurs du triangle obtusangle.
Orthocentre
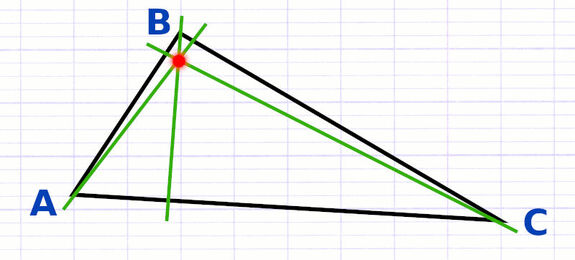
Les 3 hauteurs d’un triangle sont concourantes, ce qui signifie qu’elles se coupent en un point. Leur point d’intersection est un point particulier appelé l’orthocentre du triangle.
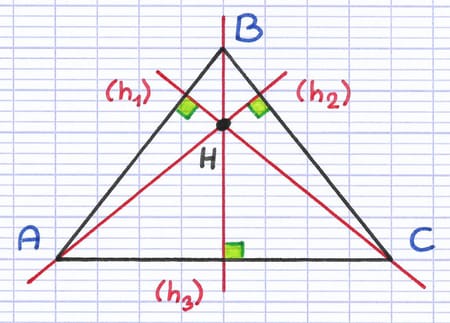
Le point H est le point d’intersection des 3 hauteurs.
Le point H est donc l’orthocentre du triangle.