Trouver une Image par Rotation et Symétrie Axiale ou Centrale
Dans cet exercice, aucune justification n'est demandée.
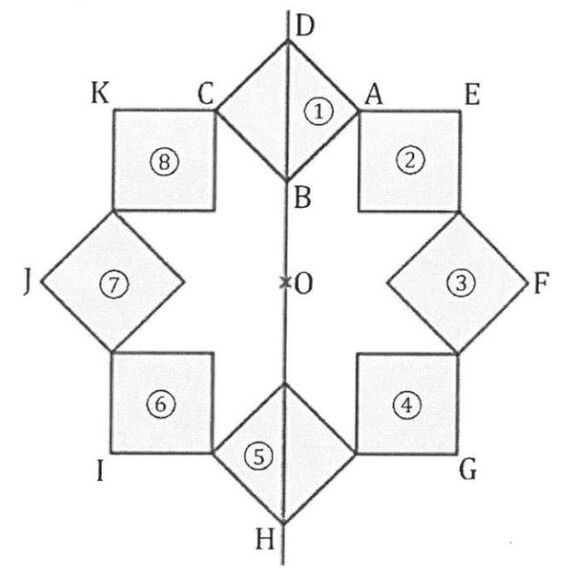
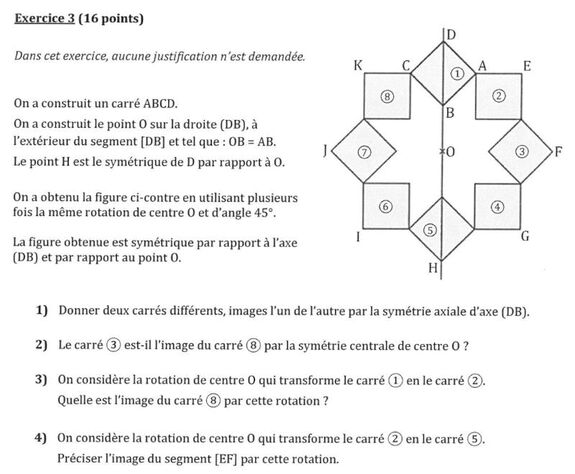
On a construit un carré ABCD. On a construit le point O sur la droite (DB), à l'extérieur du segment [DB] et tel que : OB = AB. Le point H est le symétrique de D par rapport à O.
On a obtenu la figure ci-contre en utilisant plusieurs fois la même rotation de centre O et d'angle 45°.
La figure obtenue est symétrique par rapport à l'axe (DB) et par rapport au point O.
Vidéo de correction
Vidéo de correction de l'exercice
Symétrie axiale d'axe (DB)
La première question est de donner 2 carrés différents, images l'un de l'autre par la symétrie axiale d'axe (DB). Pour trouver l'image d'un carré par symétrie axiale, il suffit de trouver les images de ses sommets. Chaque image s'obtient en traçant une droite passant par un sommet et perpendiculaire à l'axe de symétrie.
Essaye par exemple de trouver l'image du carré 8 par symétrie axiale d'axe (DB). Trace une droite passant par l'un de ses sommets et perpendiculaire à l'axe de symétrie. Reporte ensuite la distance entre le sommet et l'axe de symétrie, de l'autre côté de l'axe. Le point que tu obtiens est l'image du sommet du carré 8. Ce sommet appartient à l'image du carré 8. L'image du carré 8 par symétrie axiale d'axe (DB) est donc le carré 2.
Il est possible de trouver d'autres carrés images l'un de l'autre par la symétrie axiale d'axe (DB). Par exemple, le carré 3 est l'image du carré 7. Le carré 4 est l'image du carré 6. Tu ne peux cependant pas utiliser les carrés 1 et 5 car leur image respective est un carré identique.
Symétrie centrale de centre O
La deuxième question consiste à vérifier si le carré 3 est l'image du carré 8 par la symétrie centrale de centre O. Pour trouver l'image d'un carré par symétrie centrale, il suffit de trouver les images de ses sommets. Chaque image s'obtient en traçant une droite passant par un sommet et le centre de symétrie.
Trace une droite à partir de l'un des sommets du carré 8 et passant par le centre de symétrie O. Reporte ensuite la distance entre le sommet et le centre de symétrie, de l'autre côté du centre. Le point obtenu est l'image du sommet du carré 3. Ce sommet appartient au carré 4.
Le carré 3 n'est donc pas l'image du carré 8 par la symétrie centrale de centre O. L'image du carré 8 par cette symétrie centrale est le carré 4.
Rotation de centre O d'un carré
La question suivante est de déterminer l'image du carré 8 par la rotation de centre O qui transforme le carré 1 en carré 2. Pour trouver l'image du carré 8, il suffit donc d'effectuer la même rotation que celle qui transforme le carré 1 en carré 2.
La rotation qui transforme le carré 1 en carré 2 est une rotation de 45 degrés dans le sens horloger. Si tu effectues cette rotation à partir du carré 8, tu obtiens le carré 1. Tu peux donc affirmer que l'image du carré 8 par cette rotation de centre O est le carré 1.
Rotation de centre O d'un segment
La dernière question est de déterminer l'image du segment [EF] par la rotation de centre O qui transforme le carré 2 en carré 5. Pour trouver l'image de ce segment, il suffit donc d'effectuer la même rotation que celle qui transforme le carré 2 en carré 5.
La rotation qui transforme le carré 2 en carré 5 est une rotation de 3 fois 45 degrés dans le sens horloger. Si tu effectues cette rotation à partir du segment [EF], tu obtiens le segment [HI]. Tu peux donc conclure que l'image du segment [EF] par cette rotation de centre O est le segment [HI].
Exercice en image
Cet exercice est extrait de l'épreuve de mathématiques du Brevet des Collèges (DNB) Amérique du Nord (3 juin 2021).