Utiliser le Théorème de Pythagore, Thalès et la Trigonométrie

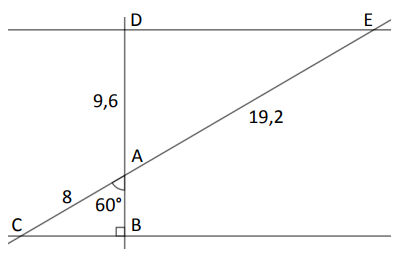
On considère la figure suivante, où toutes les longueurs sont données en centimètre. Les points C, A et E sont alignés et les points B, A et D sont alignés. La figure n'est pas représentée en vraie grandeur.

Vidéo de correction

Vidéo de correction de l'exercice

Le segment [AB] est l'un des côtés du triangle rectangle ABC rectangle en B. Tu peux déterminer la mesure du segment [AB] en utilisant les formules trigonométriques au sein de ce triangle. En trigonométrie, le cosinus d'un angle est égal à la longueur du côté adjacent divisé par la longueur de l'hypoténuse.

Au sein du triangle ABC, le cosinus de l'angle CAB est égal à la longueur du côté [AB] divisé par la longueur de l'hypoténuse [AC]. Autrement dit, le cosinus de 60° est égal à AB divisé par 8. En isolant AB au sein de l'équation trigonométrique, tu obtiens AB = 4. Le segment [AB] mesure donc bien 4 cm.

Tu peux démontrer que les droites (BC) et (DE) sont parallèles à l'aide de la réciproque du théorème de Thalès. En effet, les points C, A, E et les points B, A, D sont alignés dans le même ordre. Tu peux donc vérifier si les droites sont parallèles en vérifiant si CA / AE est égal à AB / AD.

D'une part, CA / AE = 8 / 19,2. D'autre part, AB / AD = 4 / 9,6. Si on multiplie par 2 le numérateur et le dénominateur de cette deuxième fraction, on obtient la première fraction. C'est la preuve que CA / AE = AB / AD. Les droites (BC) et (DE) sont donc parallèles.

Tu peux déduire que la droite (DB) est perpendiculaire à la droite (DE) à l'aide d'une propriété. La propriété stipule que, si 2 droites sont parallèles, alors toute droite perpendiculaire à l'une est également perpendiculaire à l'autre.

Dans cet exercice, la droite (CB) est parallèle à la droite (DE). De plus, la droite (CB) est perpendiculaire à la droite (DB). Tu peux donc en déduire que la droite (DB) est également parallèle à la droite (DE).

Le triangle ADE est rectangle en D. Pour calculer l'aire d'un triangle, tu dois multiplier sa base et sa hauteur, puis diviser le résultat par 2. Au sein d'un triangle rectangle, tu peux utiliser les côtés perpendiculaires comme base et hauteur. L'aire du triangle ADE est donc égale à (DA x DE) / 2.

On ne connaît pas la longueur DE. Tu peux cependant la calculer facilement à l'aide du théorème de Pythagore. Selon ce théorème, la longueur hypoténuse au carré est égale à la somme des longueurs des deux autres côtés au carré. Donc AE² = AD² + DE². En résolvant cette équation, tu obtiens que la mesure de DE est la racine carrée de 276,48.

Tu peux maintenant utiliser la formule de l'aire d'un triangle. (DA x DE) / 2 = 80 cm² (arrondi à l'unité près). Tu peux donc conclure que l'aire du triangle ADE est d'environ 80 cm².

Exercice en image

Cet exercice est extrait de l'épreuve de mathématiques du Brevet des Collèges (DNB) Centres Étrangers (14 juin 2022).