Additionner des Fractions (Dénominateurs Différents)

🎯

Questions validées : 0 / 3

Théorie

Pour additionner des fractions dont les dénominateurs sont différents, il est nécessaire de les placer sur un dénominateur commun. Une fois que les fractions partagent un dénominateur commun, l’addition s’effectue en additionnant les numérateurs.

★

Exemple

★

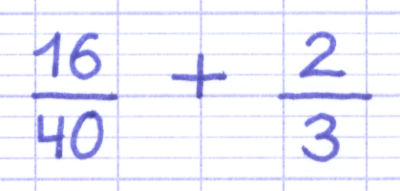
Addition de 2 fractions — Comment additionner les fractions 16/40 et 2/3 ? Ces 2 fractions possèdent des dénominateurs différents (40 et 3).

1. Simplifier les Fractions

La 1^re étape est de simplifier, lorsque c’est possible, les fractions à additionner. La simplification d’une fraction s’effectue en divisant le numérateur et le dénominateur par leur plus grand commun diviseur (PGCD). Le résultat de cette division est une fraction simplifiée égale à celle de départ. Grâce à la simplification, les prochaines étapes de l’addition sont plus faciles à réaliser, car les nombres sont désormais plus petits.

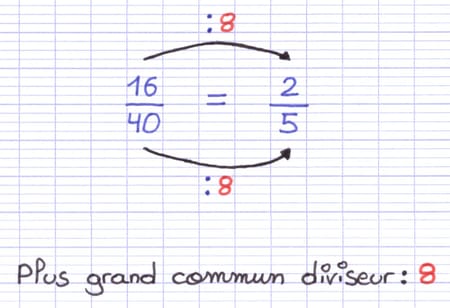
Simplification de l’une des fractions à additionner — Au sein de la fraction 16/40, le plus grand commun diviseur entre le numérateur (16) et le dénominateur (40) est 8. En divisant le numérateur et le dénominateur par 8, on obtient une fraction simplifiée (2/5).

Fiche de Synthèse

Simplifier une Fraction pour la Rendre Irréductible

L’addition des 2 fractions a été simplifiée — Au sein de l’addition, la fraction 16/40 est remplacée par 2/5. 2/3 est une fraction irréductible, il est impossible de la simplifier.

2. Mettre les Fractions sur un Dénominateur Commun

Avant d’additionner les fractions, il est nécessaire de les placer sur un dénominateur commun. Le dénominateur commun est le plus petit commun multiple (PPCM) des dénominateurs. Au sein de chaque fraction, le numérateur et le dénominateur sont multipliés par un même nombre afin de faire apparaître le dénominateur commun.

Le dénominateur commun est le plus petit commun multiple — Grâce à la liste des multiples de chaque dénominateur, on repère facilement le plus petit commun multiple (PPCM). Le PPCM est le dénominateur commun (15).

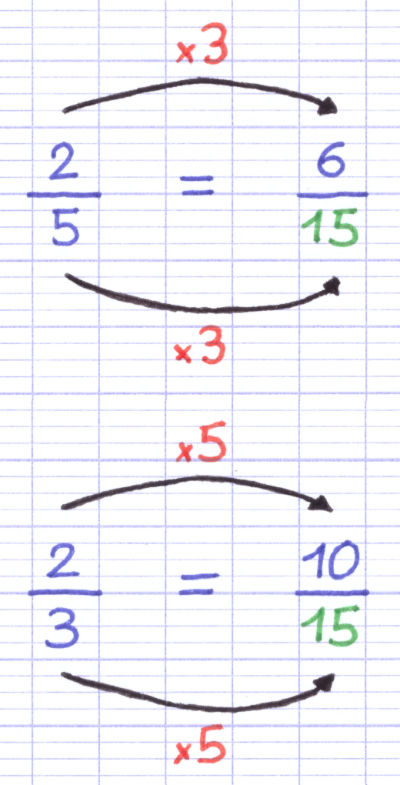
Les fractions sont mises sur un dénominateur commun — Pour mettre la 1^re fraction sur le dénominateur commun, on multiplie le numérateur et le dénominateur par 3. Pour mettre la 2^e fraction sur le dénominateur commun, on multiplie le numérateur et le dénominateur par 5.

Fiche de Synthèse

Mettre des Fractions sur un Dénominateur Commun

L’addition de fractions nécessite un dénominateur commun — Au sein de l’addition, la fraction 2/5 est remplacée par 6/15, et la fraction 2/3 par 10/15. Les 2 fractions à additionner partagent désormais un dénominateur commun.

3. Additionner les Numérateurs

L’addition des fractions s’effectue en additionnant uniquement les numérateurs. Le dénominateur commun n’est pas additionné, il est conservé au sein du résultat de l’addition.

Addition des numérateurs des fractions — On additionne les numérateurs : 6 + 10 = 16. Le résultat de l’addition est la fraction 16/15, le dénominateur n’a pas changé.

4. Simplifier le Résultat

La dernière étape est de s’assurer que la réponse obtenue est une fraction irréductible (simplifiée au maximum). Si le résultat est une fraction irréductible, l’exercice est terminé. Sinon, la fraction doit être simplifiée.