Calculer la Médiane d’une Série Statistique
Théorie
La médiane est la valeur centrale d’une série statistique rangée par ordre croissant. La médiane sépare la série statistique en deux ensembles de même effectif :
- Au moins la moitié des valeurs lui sont inférieures ou égales.
- Au moins la moitié des valeurs lui sont supérieures ou égales.
Exemple

Comment calculer la médiane de ces deux séries statistiques ?
Ranger la Série par Ordre Croissant
Pour trouver une médiane, la série statistique doit au préalable être rangée dans l’ordre croissant. La 1re étape est donc de classer toutes les valeurs de la série de la plus petite à la plus grande.

Les valeurs de chaque série sont rangées par ordre croissant.
Calculer l’Effectif Total
L’étape suivante est de déterminer l’effectif total de la série statistique. L’effectif total est le nombre total de valeurs au sein de la série.

Il y a 7 valeurs au sein de la série A.
L’effectif total est donc 7.

Il y a 8 valeurs au sein de la série B.
L’effectif total est donc 8.
Déterminer le Rang de la Médiane
On cherche ensuite à déterminer le rang de la médiane au sein de la série statistique. Pour trouver ce rang, on ajoute 1 à l’effectif total, puis on divise le résultat par 2. Le rang de la médiane est :
- Un nombre entier lorsque l’effectif total est impair.
- Un nombre décimal lorsque l’effectif total est pair.
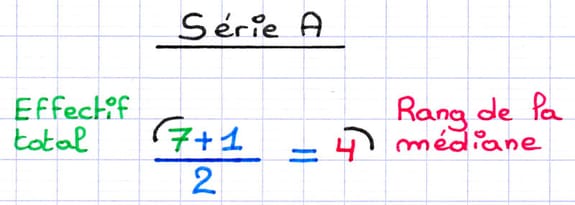
Le rang de la médiane de la série A est 4.

Le rang de la médiane de la série B est 4,5.
Trouver la Médiane
Le rang de la médiane calculé précédemment indique sa position au sein de la série statistique. Si le rang est un nombre entier, alors la médiane est la valeur située au rang correspondant.
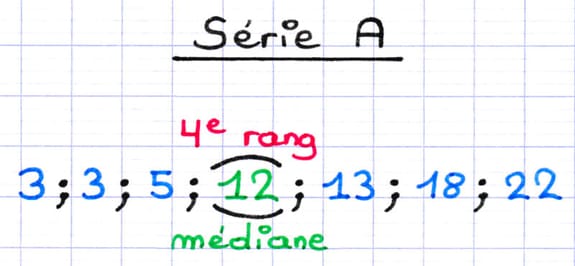
La médiane est au 4e rang de la série.
La médiane de la série statistique A est 12.
Si le rang est un nombre décimal, alors la médiane est la moyenne des 2 valeurs autour du rang correspondant. Pour calculer cette moyenne, on additionne les deux valeurs autour du rang, puis on divise le résultat par 2. Le nombre obtenu est la médiane de la série statistique.

La médiane est la moyenne des deux valeurs (8 et 10) autour du rang 4,5.
La médiane de la série statistique B est 9.
Dans ce dernier exercice, on peut constater que la médiane est parfois une valeur qui n’existe pas au sein de la série statistique. Mais dans tous les cas, la médiane sépare la série statistique en deux ensembles de même effectif.
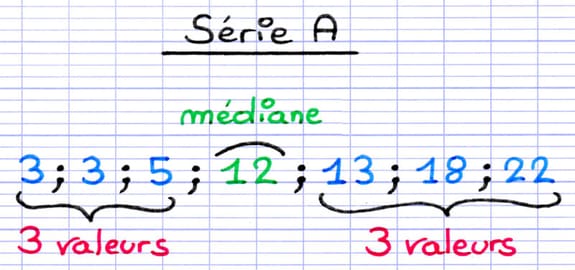
Il y a 3 valeurs à gauche et à droite de la médiane.
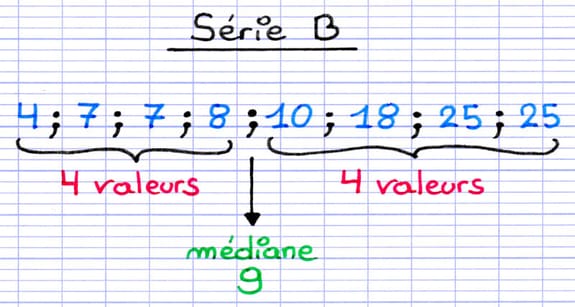
Il y a 4 valeurs à gauche et à droite de la médiane.

